Recently I was working on a project that involved using meshes with planar faces. In most cases we use normal meshes and the employ different techniques of mesh planarization. These techniques often use different optimization techniques such as forced base algorithm for relaxation or gradient based minimizations to move the vertices of the mesh slightly from the initial position and reduce the non-planarity of the mesh cells. The success of these techniques are heavily depending on the size and topology of the input mesh as well as the magnitude of mesh non-planarity.
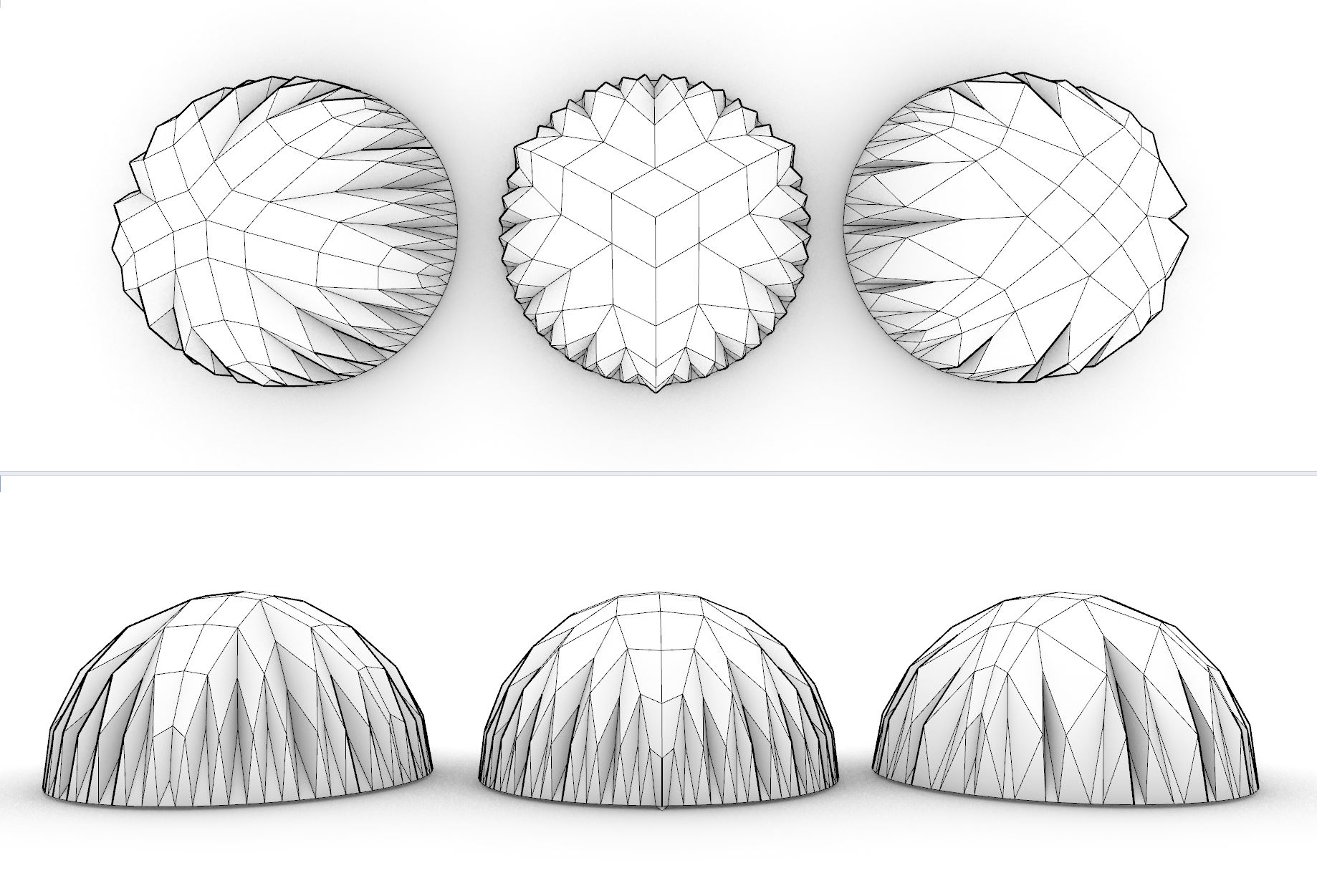
Another approach to planar meshes is to create the meshes with planar faces at the first place. An example is the Quad Mesh Dome which contains the Planar Quad faces. This object is created using dynamic programming technique. It starts with an initial pattern on the top which contains arbitrary number of planar quads. Then in the next row, two faces are created in the space between the upper faces. In creation of the new faces the position of the shared vertex is calculated as such that both quad faces stay planar. This process repeats for all two consecutive faces in the current row until 2*n faces are created in the next row. Then the problem is redefined as the faces of the new row become the input for the faces for the next row.
The result is a mesh (dome) which contains always planar faces. A mesh with planar quads is very useful in architectural design.

Recent Comments