Signed distance of a point from a plane

by | Feb 29, 2020 | Revit Programming | 0 comments

Today I was looking at the Project() method in Revit API. The method signature offers a distance parameter which outputs the distance of the projected point to the input point. 

public void Project(
	XYZ point,
	out UV uv,
	out double distance
)

 The value of distance parameter is always positive which means we have no clue if the point is above or below the plane. Apart from this issue , the method is implemented in Revit API 2018.1 and it is not available in earlier versions. In this post I discuss two different methods for finding the signed distance of a point from a plane, first using change of basis and trasformations and in the second method we use dot product which in my opinion it is the essence of linear algebra! 

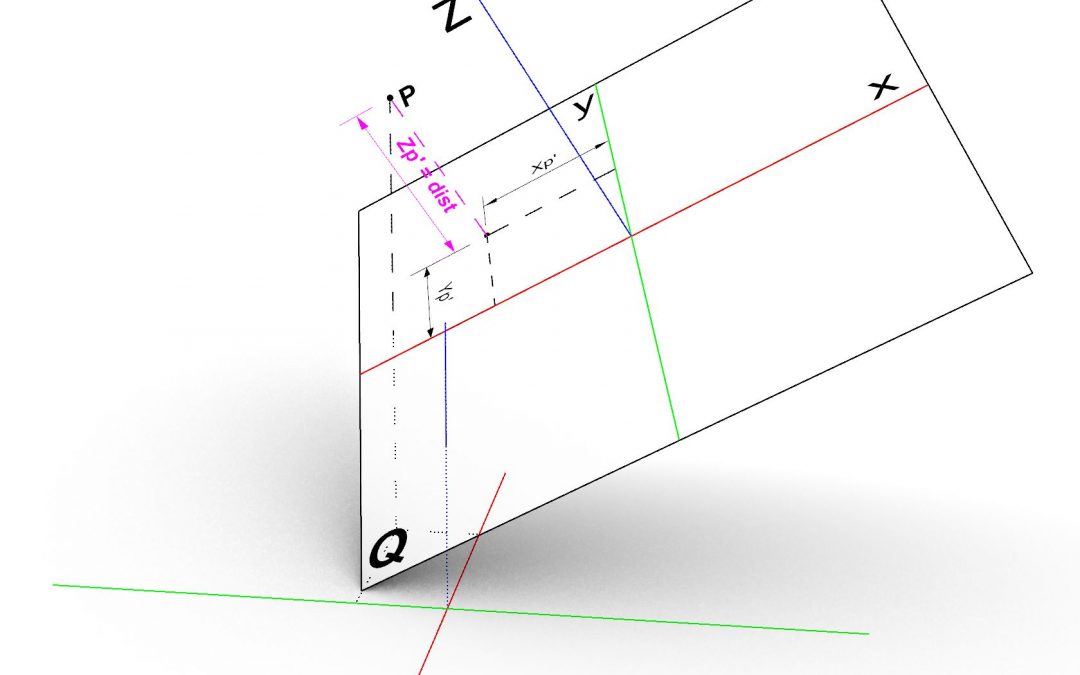
In order find the signed distance of point p from the given plane Q we can simply evaluate the point with respect to the local coordinate system of the plane. This operation is called change of basis. Let us say the plane Q is at origin O with basis X,Y and Z, We can write the components of the plane Q in vector format :

 

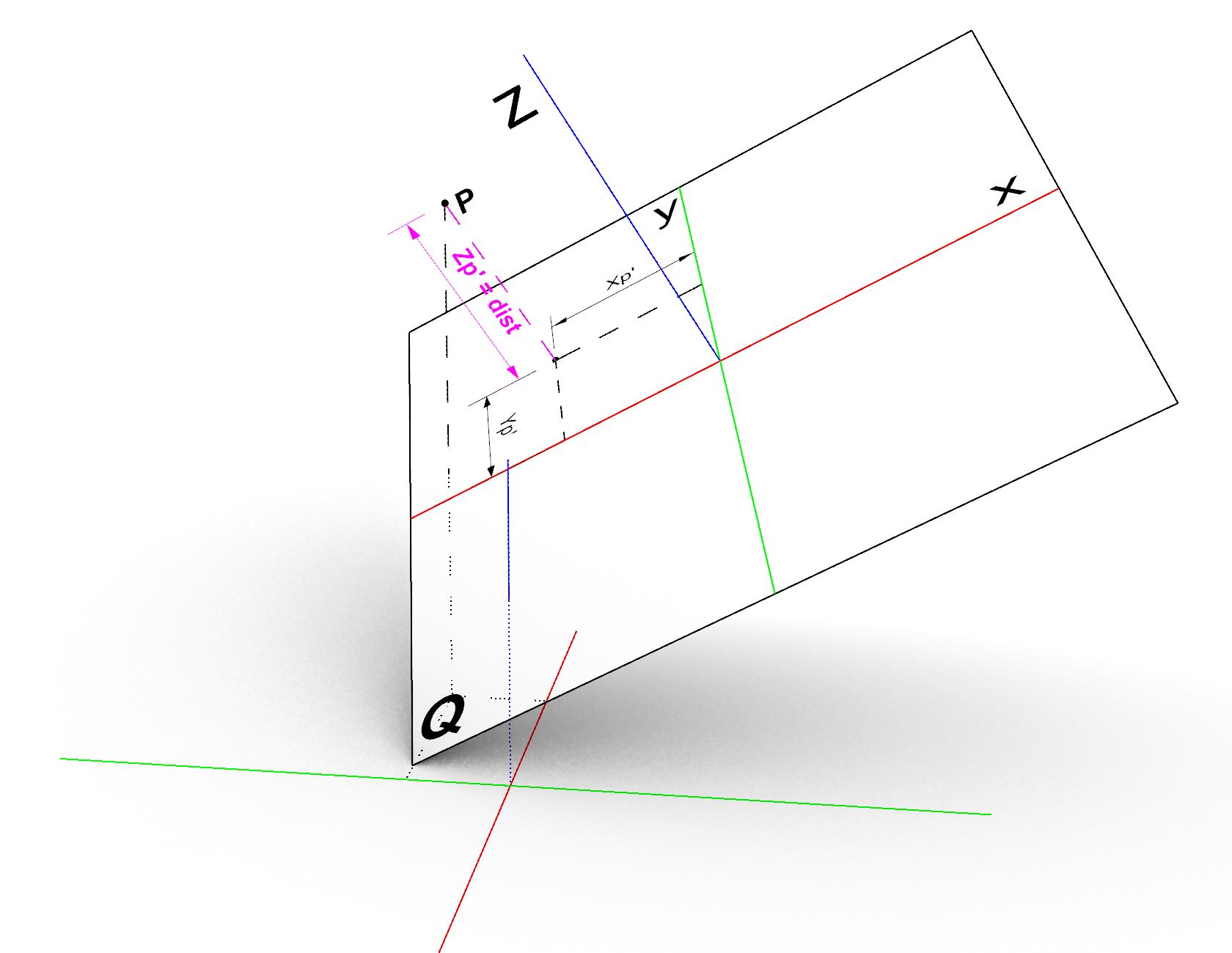
The transformation of any point from global coordinate system to the plane coordinate system can be define by the 4×4  matrix A which is composed of the basis vectors of the plane and the origin point (translation part).

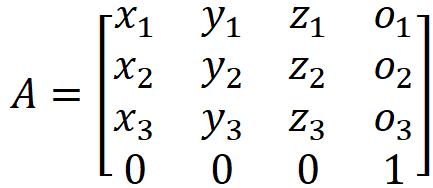
The point p’ is described in the plane local coordinate system, therefore by transforming p’ to using plane transformation we obtain point p in global coordinate system. This operation can be reversed to find the point p’ which is the coordinates of point p with resepct to the plane coordinate system.

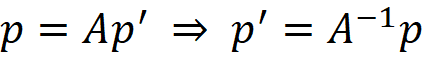
Below snipped code demonstrates the implementation of change of basis and extracts the Z coordinate of point p’ as the signed distance of the point p with respect to the plane. Also note that we can output the projection point just by transforming the local projection of p’ to the global coordsys.

        /// <summary>
        /// return signed distance of point from the plane. 
        /// If the point is above the plane (in positive side of the plane) 
        /// the result is positive and if the point
        /// is below the plane the result is negetive
        /// </summary>
        /// <param name="plane">Input plane</param>
        /// <param name="point">Point to measure the distance from</param>
        /// <param name="projection">Projection of input point on this plane</param>
        /// <returns></returns>
        public static double DistanceTo (this Plane plane,XYZ point,out XYZ projection)
        {
            //build a transformation matrix based on the plane coordinate system
            Transform tr = Transform.CreateTranslation(plane.Origin); 
            tr.BasisX = plane.XVec.Normalize();
            tr.BasisY = plane.YVec.Normalize() ;
            tr.BasisZ = plane.Normal.Normalize();
            //Find the local coordinates of the given point with resepct to plabe coordinate system
            XYZ local = tr.Inverse.OfPoint(point);
            //project the local point to the XY plane (Z=0)
            projection = new XYZ(local.X, local.Y, 0);
            // transform the projection back to the global coordSYS
            projection = tr.OfPoint(projection);
            //The Z coordinate of the local point is the signed distance from the plane 
            return local.Z;
        }

Well, above is not really an elegant method!, my aim was to discuss a bit of change of basis which is very important topic. The distance of a point from a plane is simply calculated from the equation (5) in below.  Let us assume plane Q with normal n  and a point on plane p0  and a point p outside the plane with its normal projection on plane p’. 

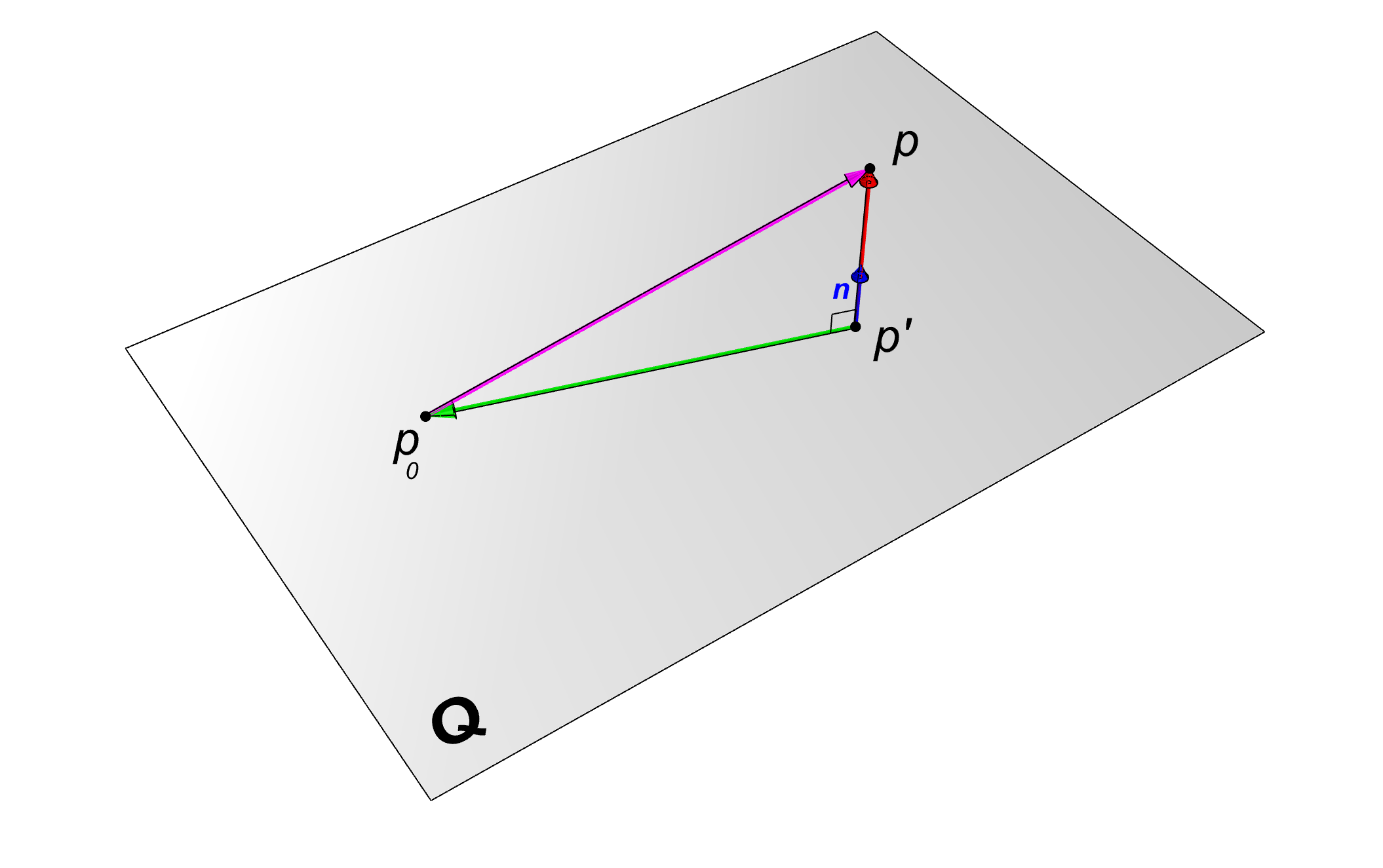
Starting from equation (1) which is simply sum of vectors and taking dot product of both sides we obtain equation (2).  

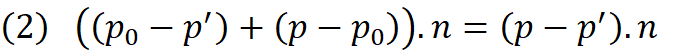
Equation (3) is obtained by expanding (2) and rewriting (p-p’).n as d*n where d is the distance between the p and p’ (Note if p is below the plane then d must be negative therefore d is signed distance). Then we can write (4) by replacing (p₀-p’).n with zero since two vectors are perpendicular and their dot product is zero.

Finally in we replace n.n by 1 since n is normal vector. Equation (5) gives us the signed distance from the plane and by moving the point p in opposite direction of plane normal (n) by the magnitude of d we obtain p’ in equation (6)

Below is a simple and more elegant implementation of the same method. 

public static double DistanceTo2(this Plane plane, XYZ point, out XYZ projection)
{
    // signed distance from equation (5)
    double d = (point - plane.Origin).DotProduct(plane.Normal);
    // the projection point from equation (6)
    projection = point - d * plane.Normal;
    return d;
}

Submit a Comment