Today I saw a question on Para-3d forum which I found interesting in the topic of the transformations. Here is the equation :
Question:
Hi! Please help to understand how to accomplish the task:
I have an array(1d) of instanced shapes along path-spline.
Starting shape has 100% size and end one is of 20%
What should I rearrange to eliminate gaps between gradually diminishing shapes aligned to path? At the same time I do not want to have my shapes deformed in any way (by FFD and other means)Bounding box button of linear controller is not active in my case. Please see attached images.
Sorry but I could not upload images directly to the forum – it does not work, please check, and my illustrations for the question are here:

Here I redefine the problem so that we can take right approach to the solution.
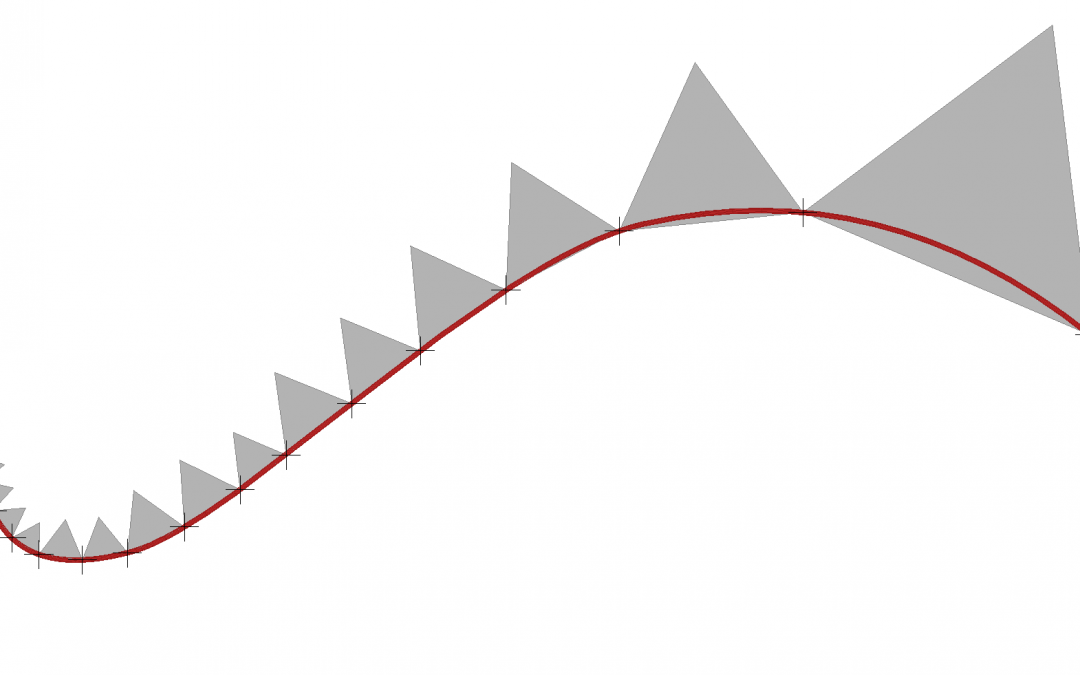
Th triangle object is arrayed on a 2D curve and it is scaled to fit in each division. The problem has two parts, First dividing the curve into uneven divisions that are gradually increasing in size from one end to other, the second part of the problem deals with fitting the triangles within each division.
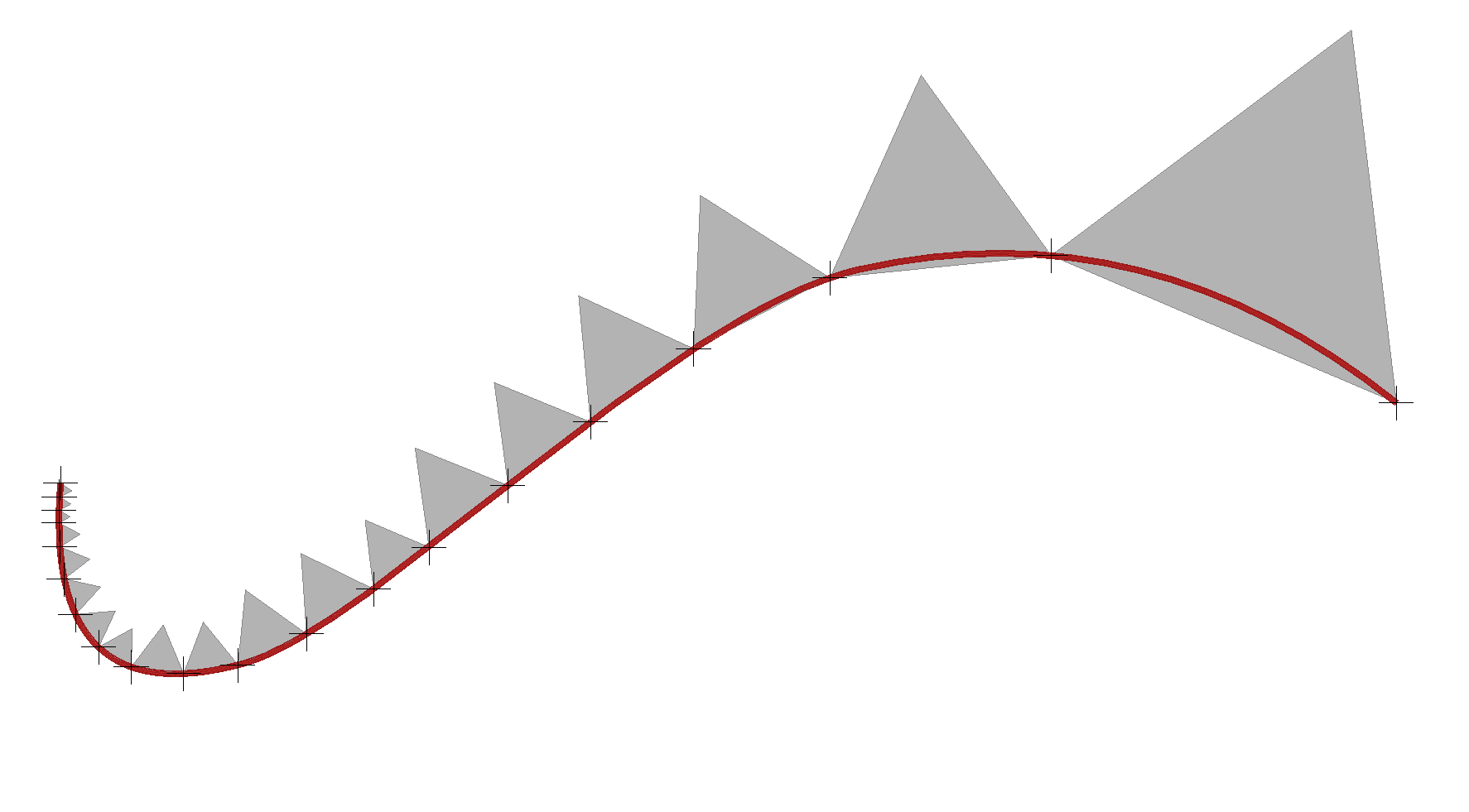
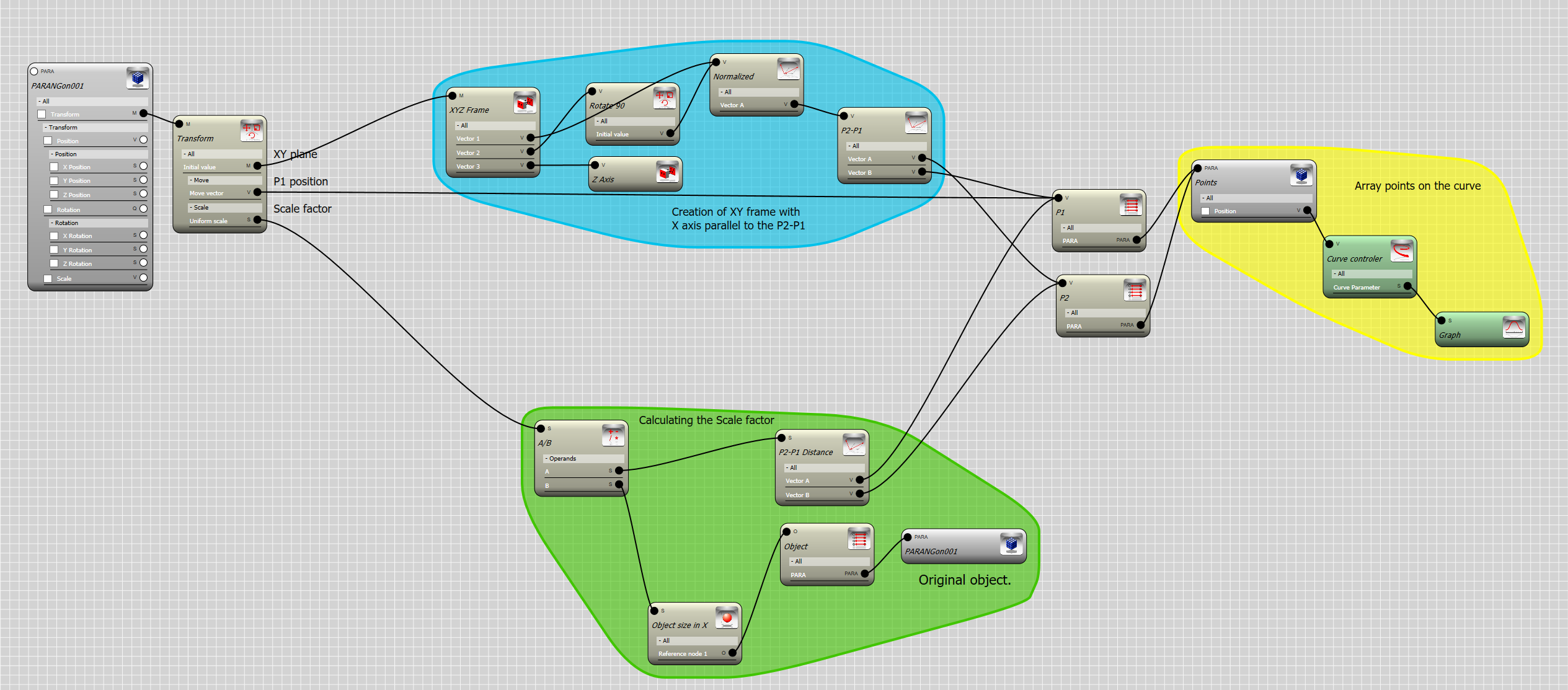
Two divide the problem into above mentioned parts, we first array points (Helper object) on the curve and then in the next part we use these points to array the triangles.
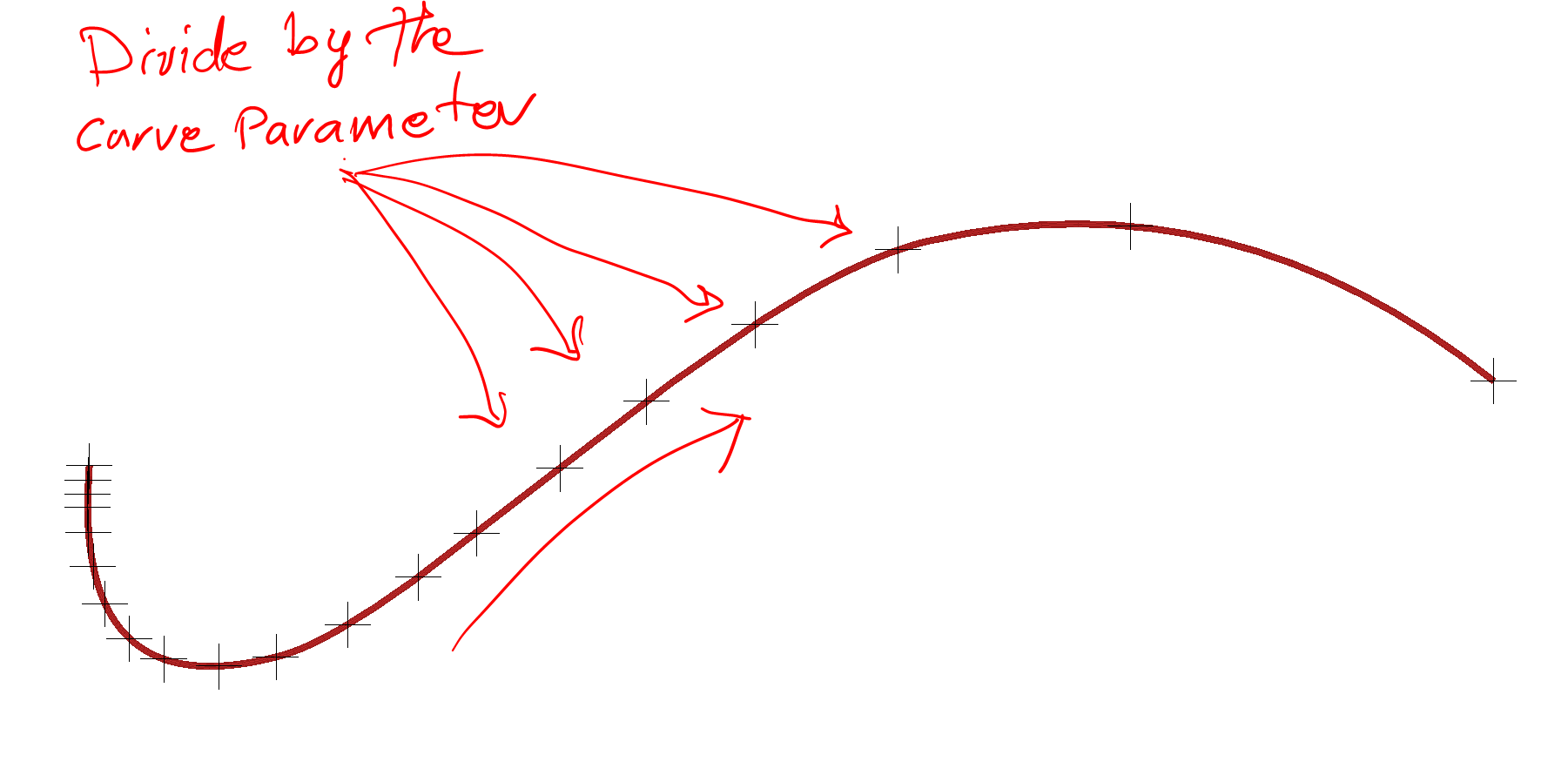
Now with points we solve the first problem : We have a curve in 2D space which must be divided in an uneven manner. So first step is to find a way to control the length of the divisions. The Curve controller in Para-3d offers several ways to do subdivide the curves , such as divide by number, divide by curve length and divide by curve parameter. Here I should use Curve parameter instead of default divisions so that I can alter the spacing along the curve.
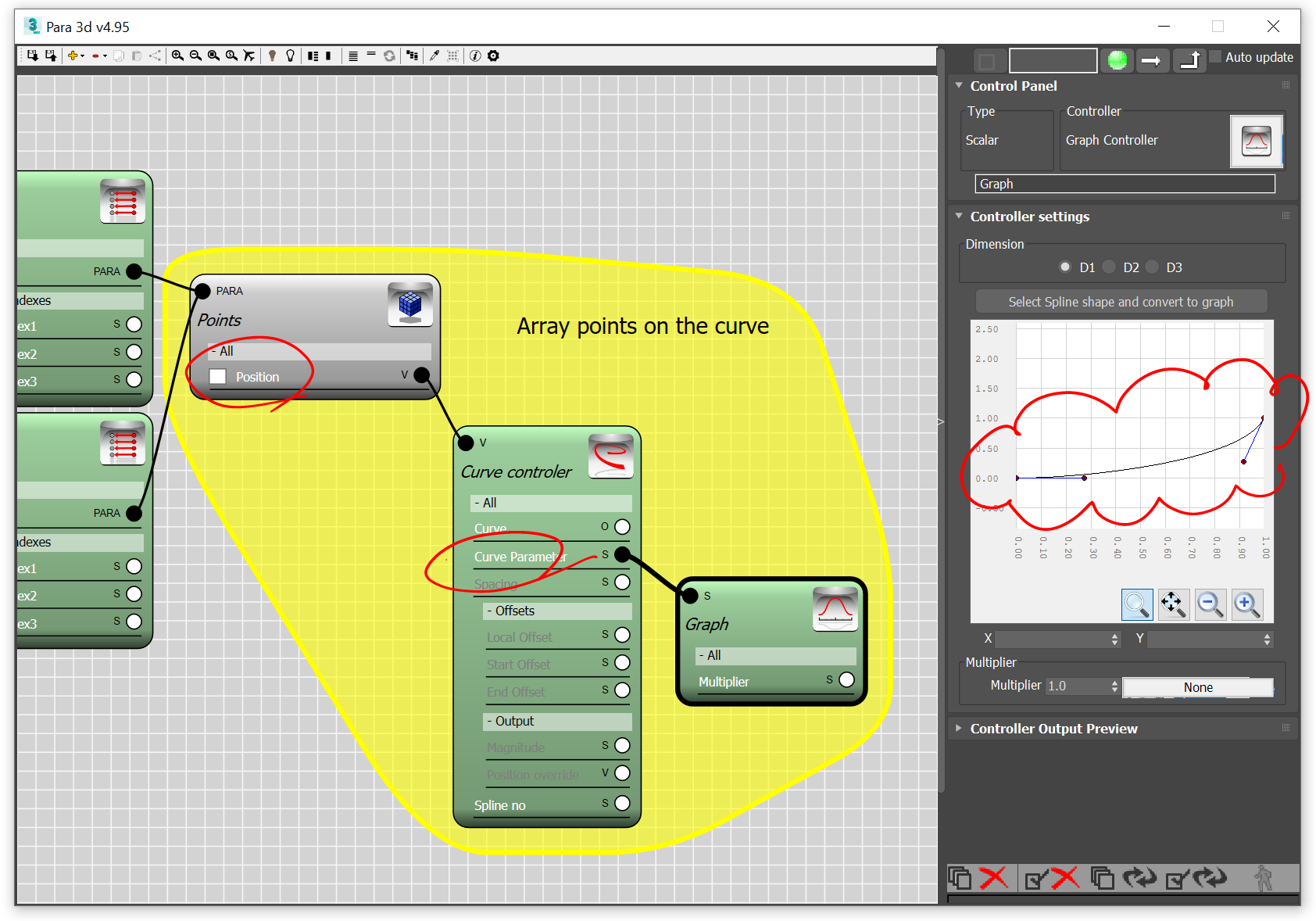
Notice in above Para flow, the Graph is controlling the Curve parameter, and the spacing between the points are gradually increasing by the graph from 0 to 1. If graph was a straight line then the gap between points would have been almost equal.
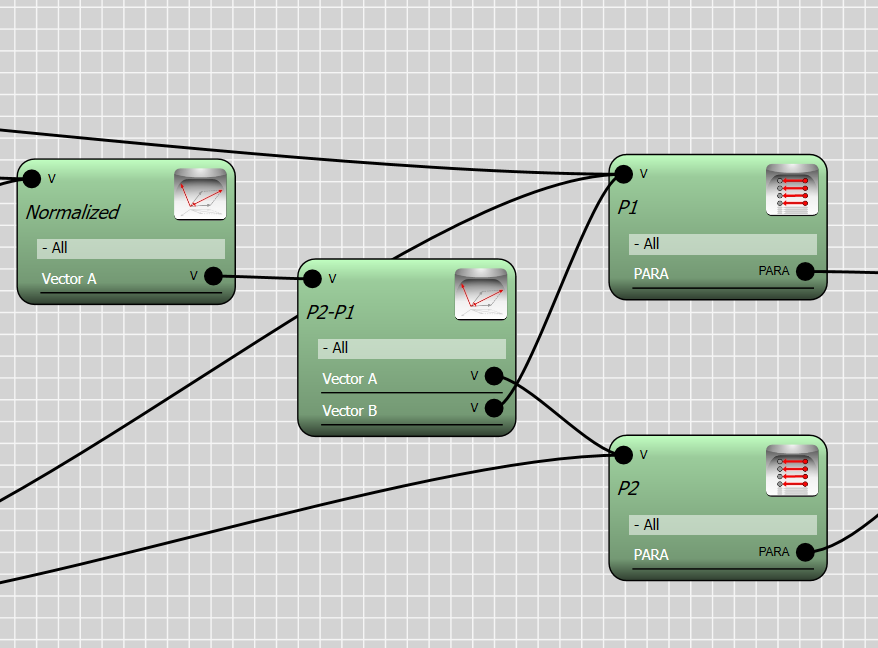
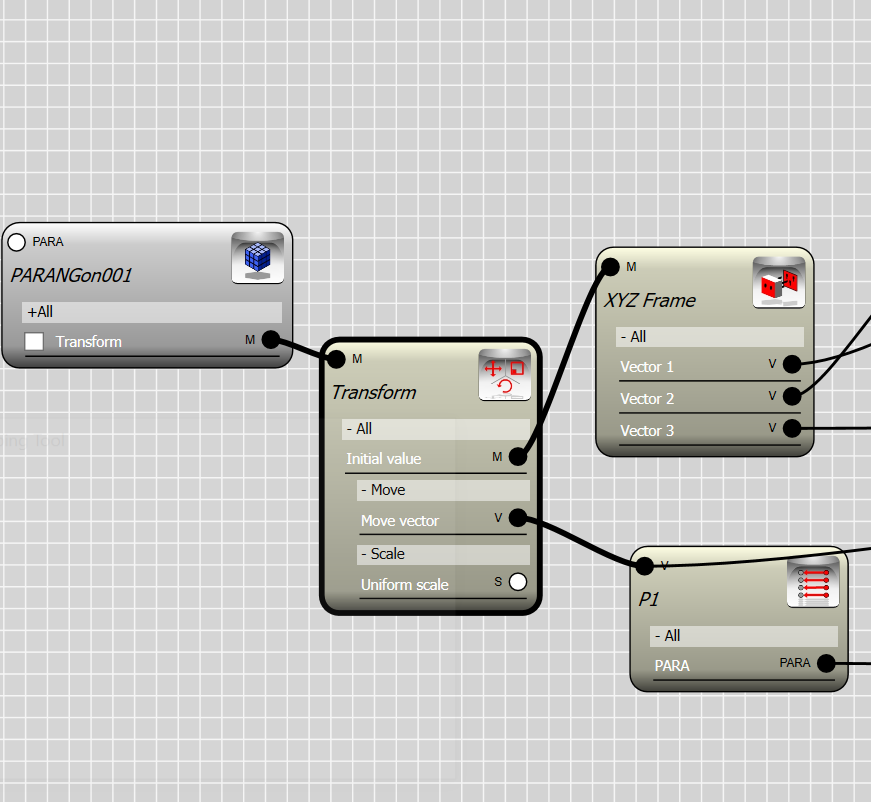
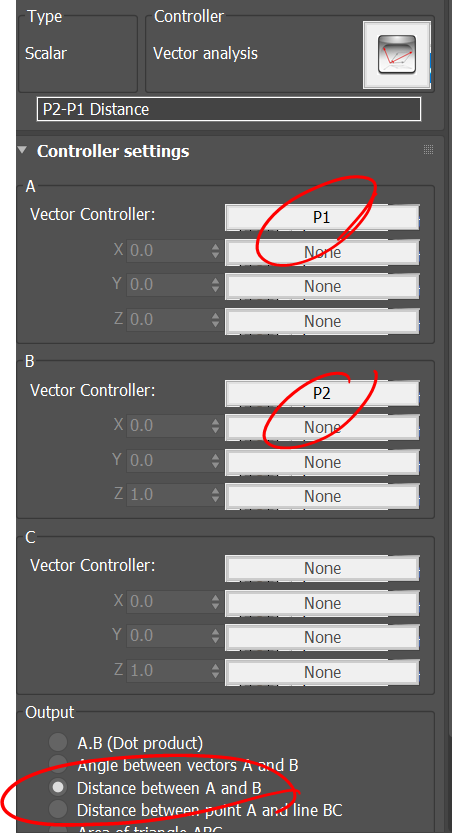
The second step is to array the object in such a way that it fits between two consecutive points. For each object we look up two points, let’s say P1 for the corresponding point and P2 for the the next point in the array. This is done by Para-Link controller.
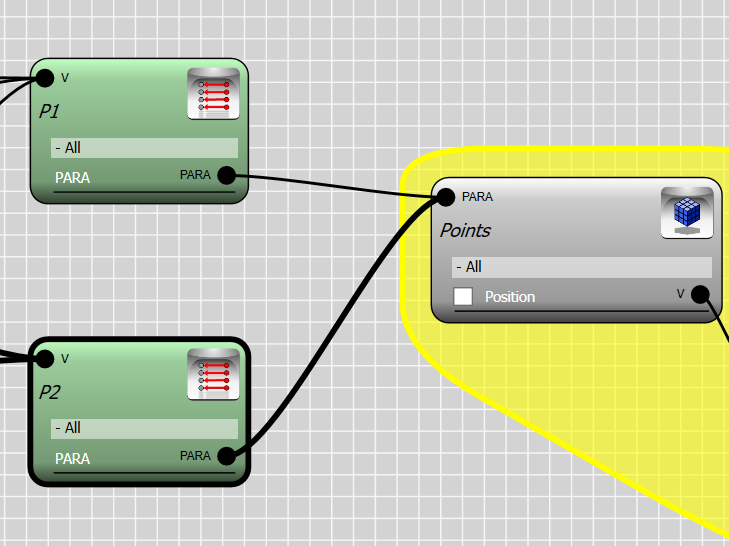
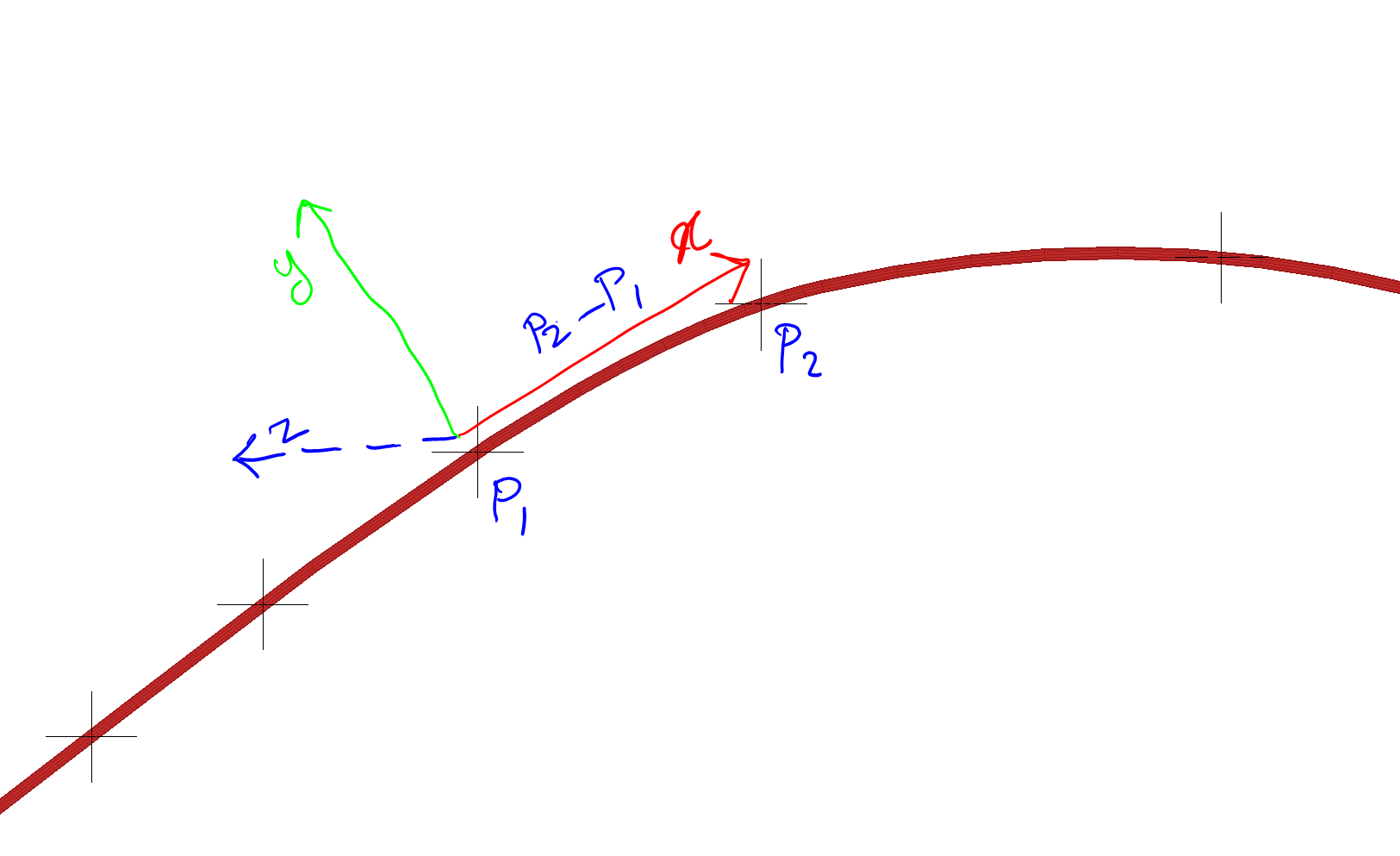
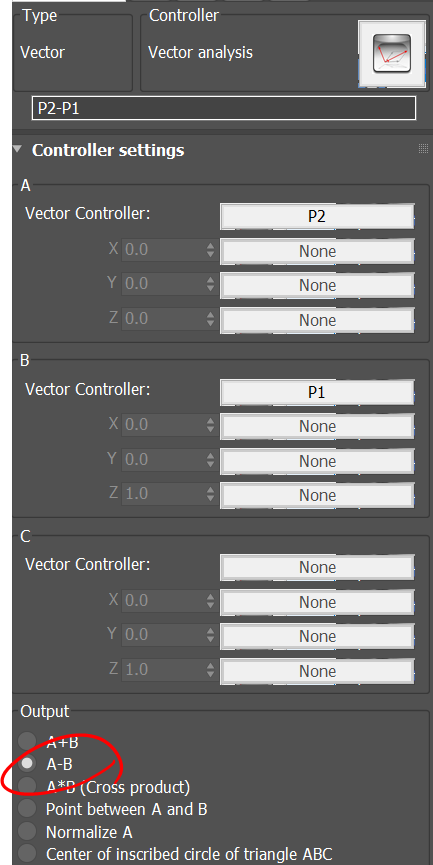
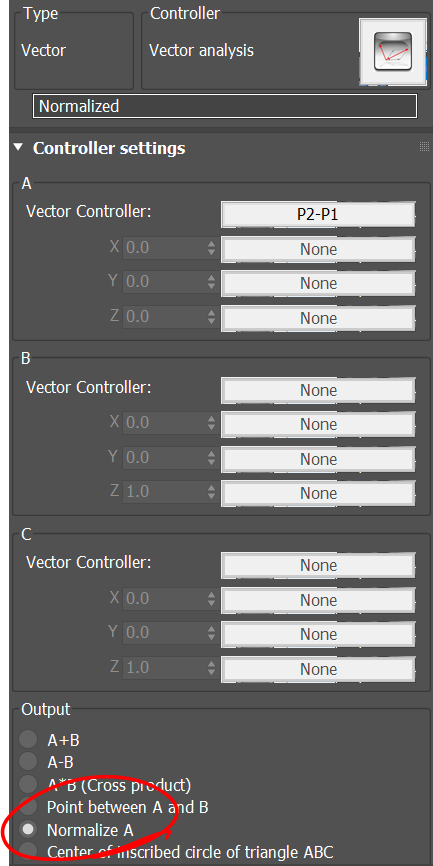
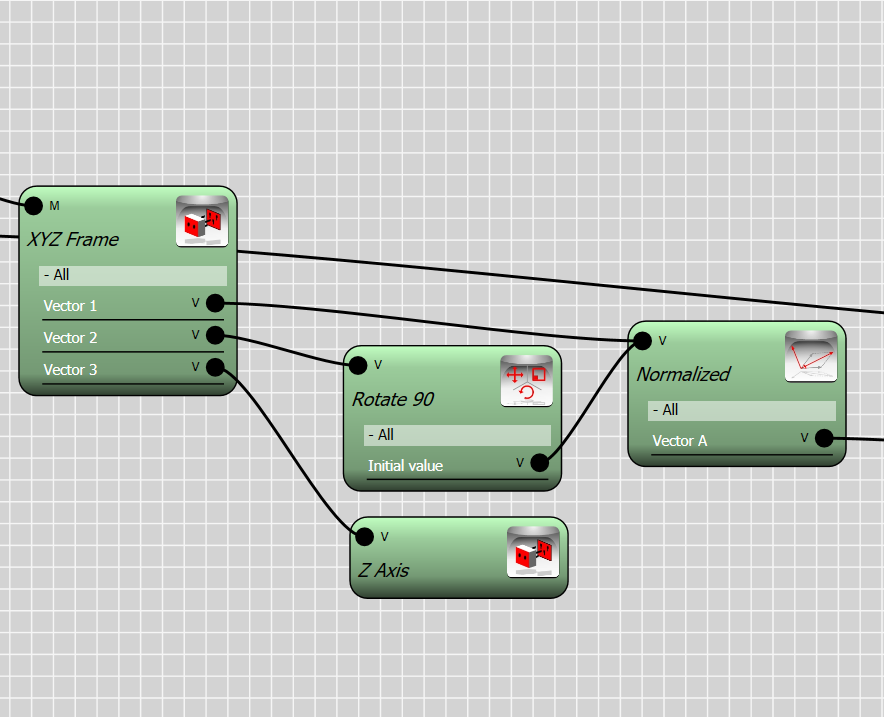
We now construct a vector which connects point P1 to P2. This vector is used to create a plane which the object will fit into. We normalized the vector P2-P1 so it does not affect the scale of the object. Both operations can be done by the vector controller.
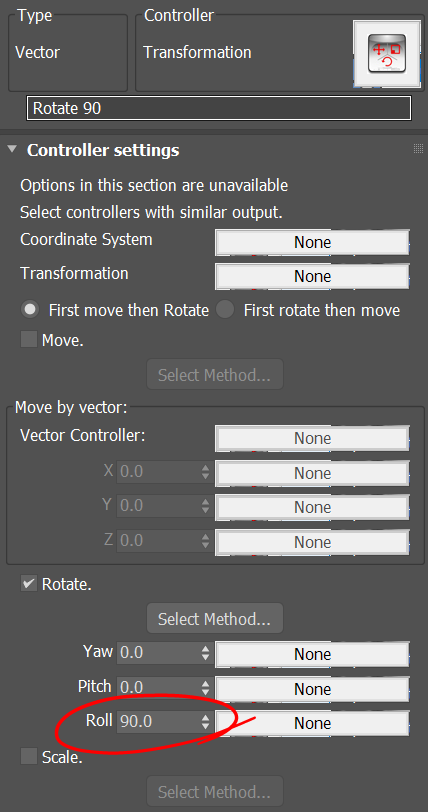
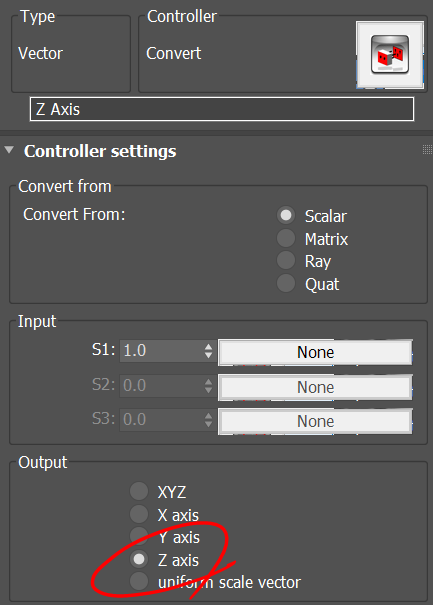
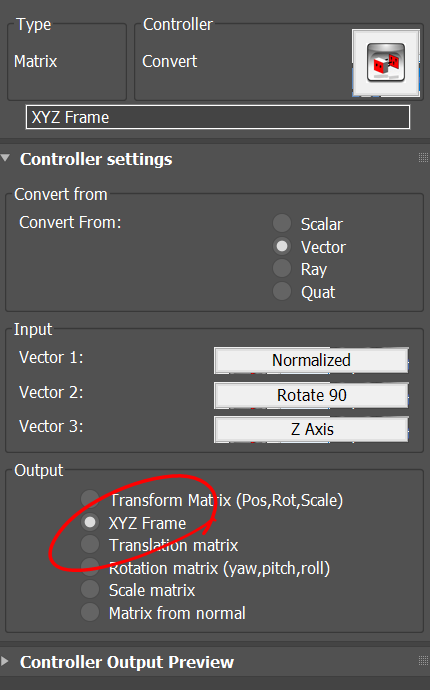
To construct a frame we require 3 vectors. The X basis of the frame is given by the vector P2-P1 and the Y basis is the same vector but rotated 90 degree. We use the global Z axis for the Z basis since the curve is in XY plane.
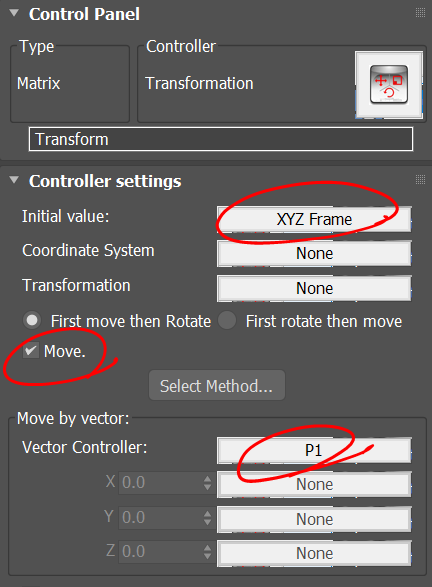
The XYZ frame is created by the convert controller which converts 3 given vectors to a frame. we also use a Transform controller to rotate the X basis .
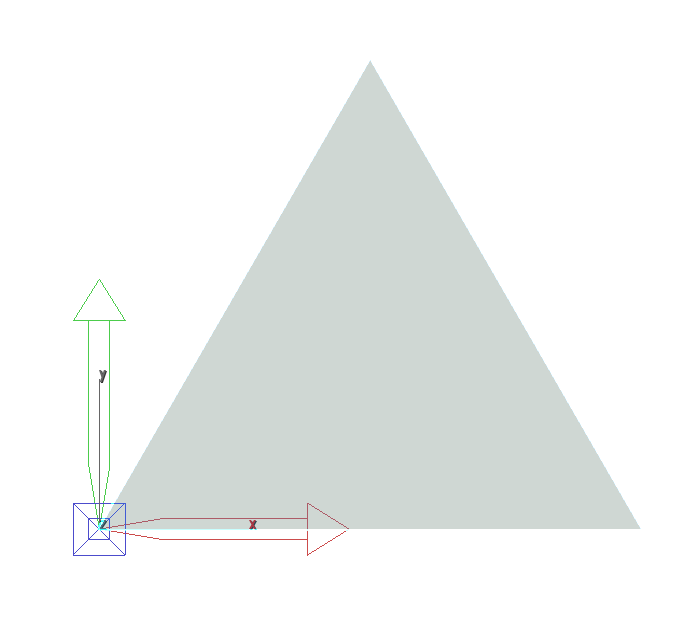
Now that we have constructed the frame , we can use it to position and align the triangles , however, the triangle must have its X local axis along the lower edge and its local origin at the lower left corner as it is shown in the above.
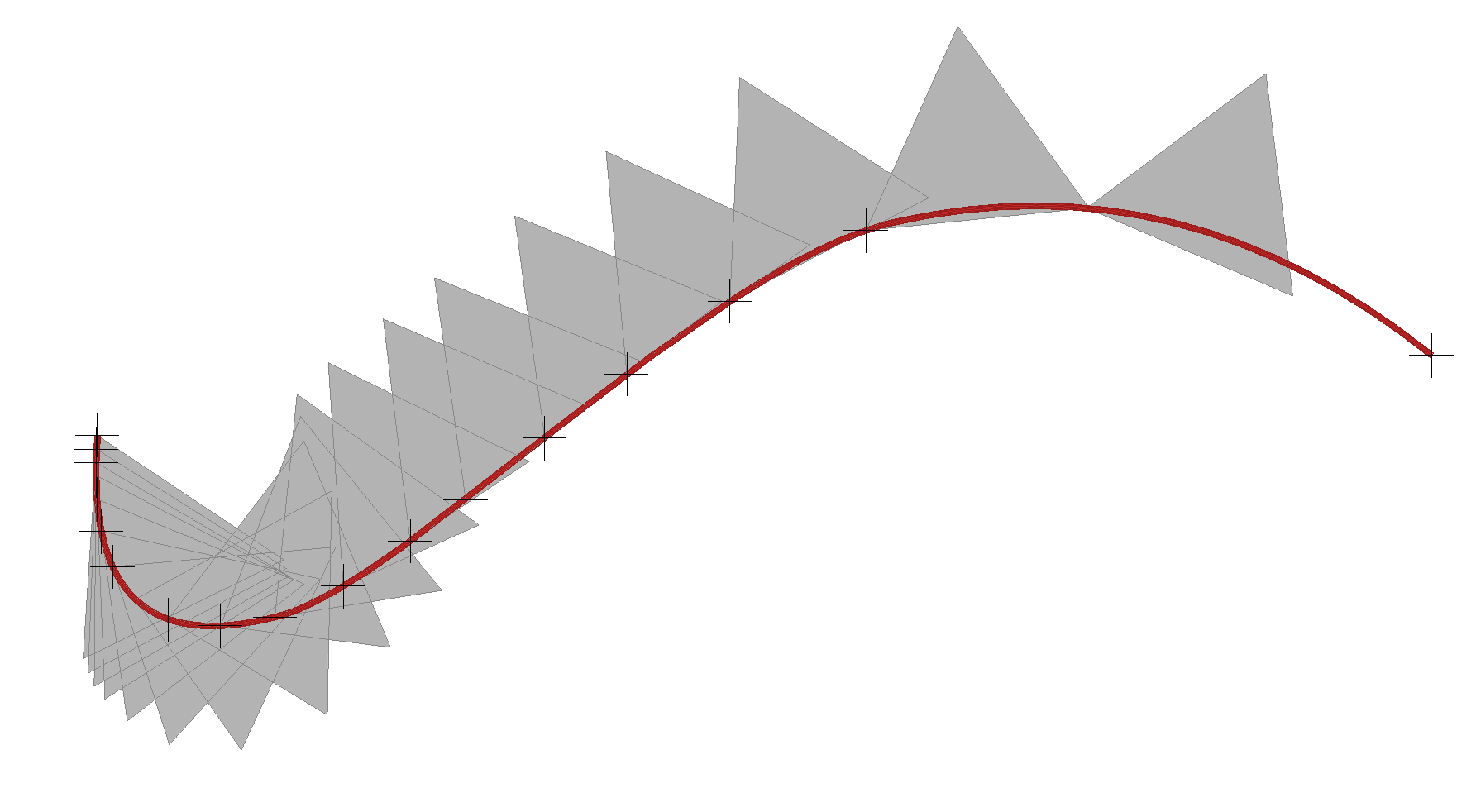
Trandform controller takes an initial transformation as input and perform further transformations. This is similar to multiplication of transformation matrices from left to right.
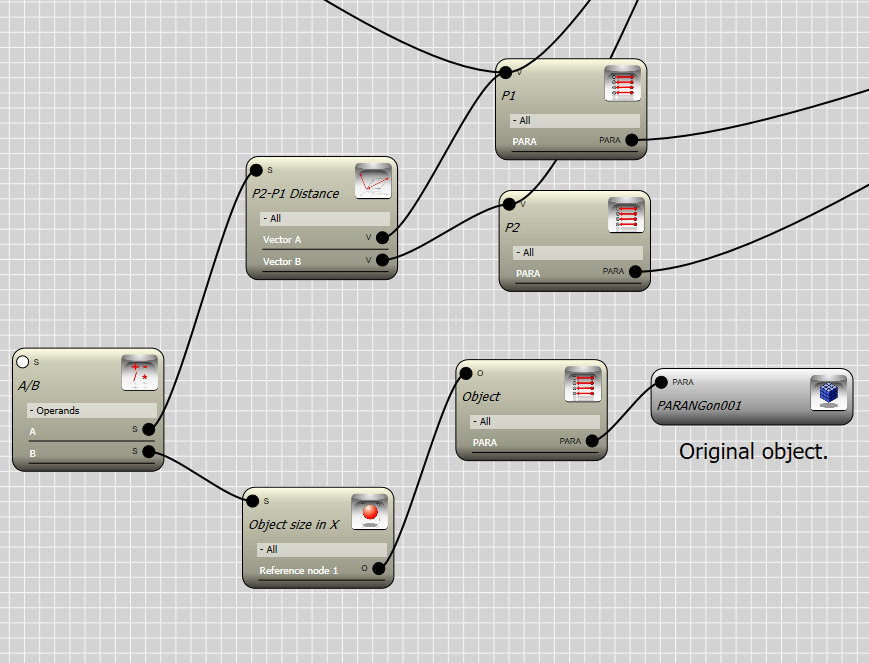
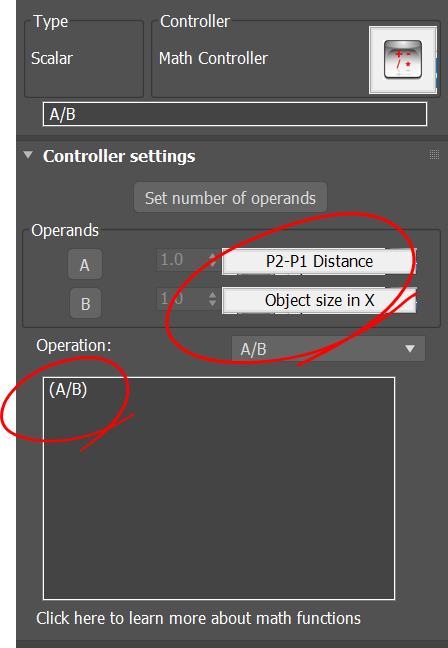
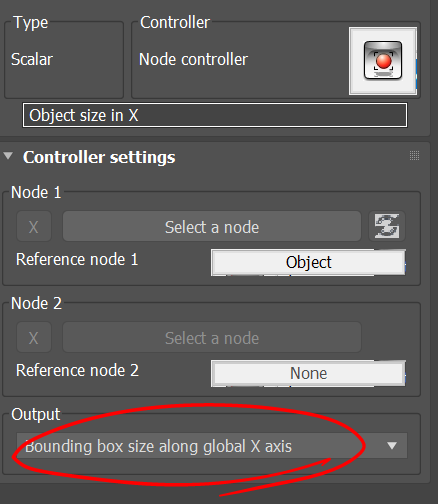
Last step is to scale the object in order for it to fit between points P1 and P2. Here we need two measurements, one is the distance between P1 and P2, and the second is the size of the object along its local X axis. Once we have these two dimensions , we can divide the distance |P2-P1| by the object size and find the scale factor. In below you can see how this is done using Para-3d controllers.
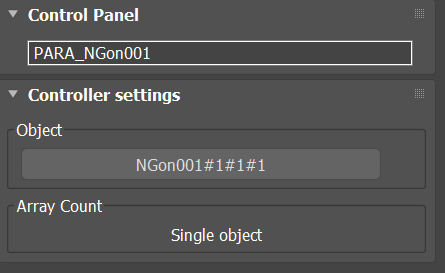
Note that to obtain the object size we need to keep a copy of the original object. The original object the is assigned to a Para container to measure its size in local X axis.
Adding the scale factor to the transform controller makes our graph completed.
I hope this explained the process of the transformation. We combine all sort of transformations including
- Alignment using XYZ Frame
- Move
- Rotation
- Scale
Please feel free to comment if you didn’t follow me 😉

Recent Comments