Plane and Curve intersection

Plane-Curve intersection from algebraic point of view is quiet similar to Plane-Line intersection which we discussed in previous post. In this post I would like to take the same approach in finding the Plane-Curve intersection which involves root finding techniques, and in the next post we will also look at Face-Curve intersection method and we will use to implement a method for Plane-Curve intersection. If you are looking for a robust and fast solution , then feel free to jump to my next post . If by any chance you are interested in differential geometry and mathematics like me 😉 then please continue reading… 

Let’s have a look again at the plane and curve parameterization: 

Equation (1) represent a plane with normal vector n which passes through point p₀ and Equation (2) is the parametric formulation of curve C with parameter t. C is a function which maps a real number to a position vector in 3d space. In this form t is called natural parameter of curve C.  P represents the point on plane and the point on the curve in both equations, just like the Plane-Line intersection we replace the point p in  equation (1) by its value from equation (2) and we solve the new equation for t. 

In order to solve above equation we need to know about the function C in Revit API. There are two methods which can be used to evaluate the curve with given natural or normal parameter which are listed below  

The first method simply evaluate the curve at given parameter and return the point on the curve. The second method is far more better, since it returns the potion of the point along with its derivatives which are useful in root finding technique which we will discuss later. Please read documentation for ComputeDerivatives() as I’m not going to cover all details here.

The equation (3) has one unknown (t) and if the curve is smooth and differentiable then the equation is also differentiable which means we can use newton method for root finding . Although there are several roof finding algorithms which can be used in this case, but I have selected the newton method as it is easy to implement and has quadratic convergence rate. As I mentioned above you may not use this algorithm for your code where the Plane-Curve intersection is used expensively and instead, please refer my next post on this topic. 

The newton method requires to have the first derivative of equation (3) with respect to the unknown (t). Here we shall write:   

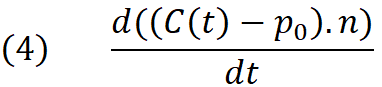
Expanding above we get : 

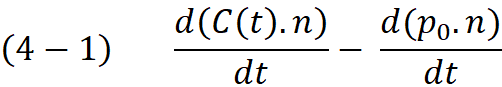
The second part is constant with respect to the t , therefore it is eliminated

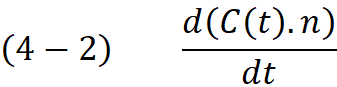
Expanding the (4-2) using the derivative of the dot-product we obtain: 

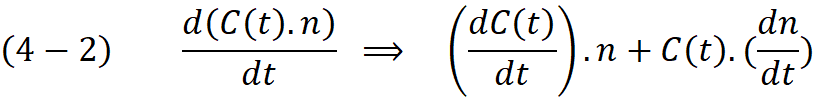
Again the right expression is constant with respect to the (t) therefore we can eliminate and write :

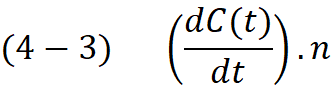
In equation (4-3) we only need to the derivative of the function C with respect to the parameter t and then compute the dot product of it with plane normal. As already mentioned above the ComputeDerivatives()method returns the first derivative of the function C in the BasisX vector of the resulted transformation matrix. This derivative can be also interpreted as the tangent vector to the curve at parameter t. Now we have both requirements for Newton method, first the evaluation of the equation (3) which we call it function f(t) from now on and the first derivative of the function f at parameter t which is written as df : 

I’m not going to discuss the newton method in full detail , The most basic version starts with a single-variable function f defined for a real variable x, the function’s derivative f ′, and an initial guess x₀ for a root of f. If the function satisfies sufficient assumptions and the initial guess is close, then:

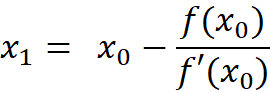
The algorithm is pretty simple, we start with initial guess t and in each iteration we compute the step size dx = -f(t)/f'(t) . The parameter t is moved to the new position and the function f is evaluated again. This loop continues till either the value of function f is close to zero or the number of iteration exceeds a maximum value (here 100 iterations) . Below shows the implementation assuming the interval [t₁,t₂] is the curve domain.  

To implement the method we need a guess point, a point which grantees that algorithm finds a root. This depends on choice of t and number of solution of equation (3).  It is possible for a curve that intersect the plane in more than one point, this means we need to run the root finding algorithm in the intervals which we know one local solution is available. Almost all root finding algorithms finds only one solution near the guess point , therefore another algorithm must be implemented to find the intervals with only one root. This is generally called root isolating algorithm where in most cases require the original polynomial of the function f(t). Unfortunately we are not able to retrieve the polynomial function via Revit API. However there are methods in Revit API which allows to split an divide curves. 

Using MakeBound() we can create a curve from a sub-domain of the bigger curve C. Since we are using the curve parameter t in function f(x) dividing the curve C at parameter t is the same as splitting the function f(x) using line x=t . 

Some algorithm suggest to approximate the curve with retentively small segments and then run the root finding algorithm in each segment. Since with Revit API we can compute the curve length in each step, I’m going to take advantage of this known parameter. We start with subdividing the curves into half till a certain conditions are met. The first condition is that we ensure there is at least one root for function  f(t) . We know that If f(t)=0 has odd number of solutions then f(0)*f(1) <0  (the graphs on the left) and if the number of solution is even or has no solution then f(0)*f(1) >0 holds (the graphs on the right).

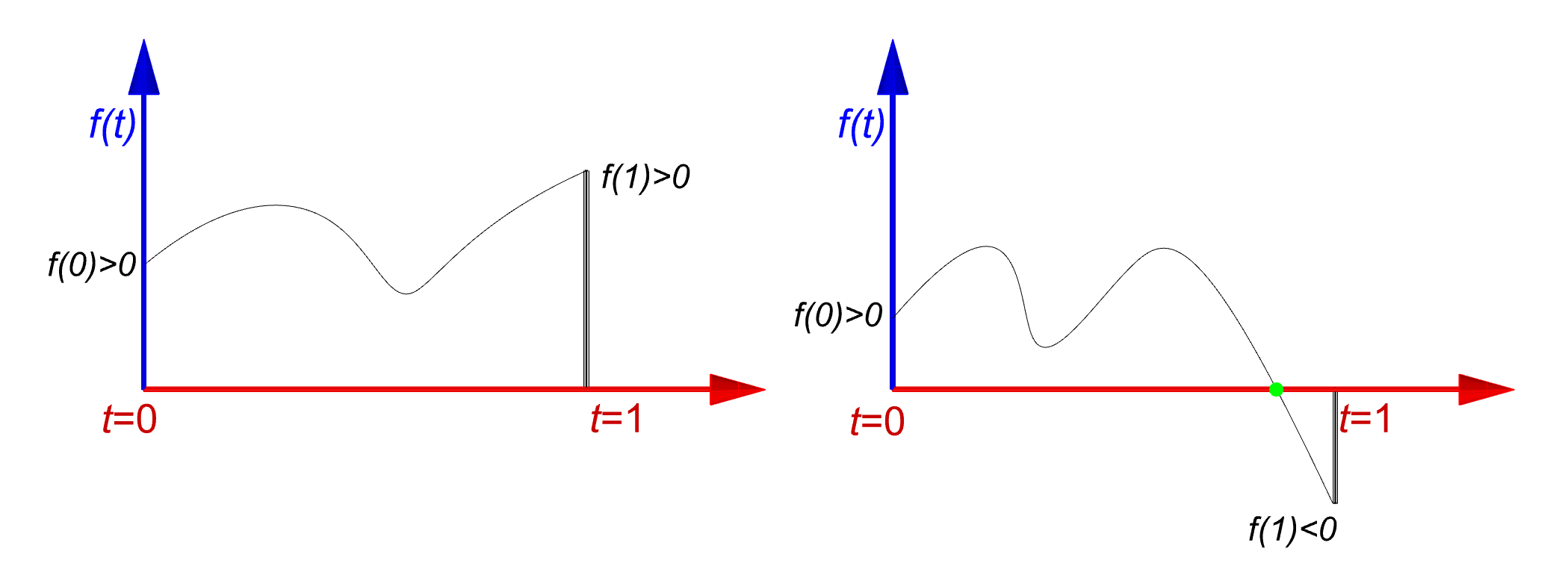
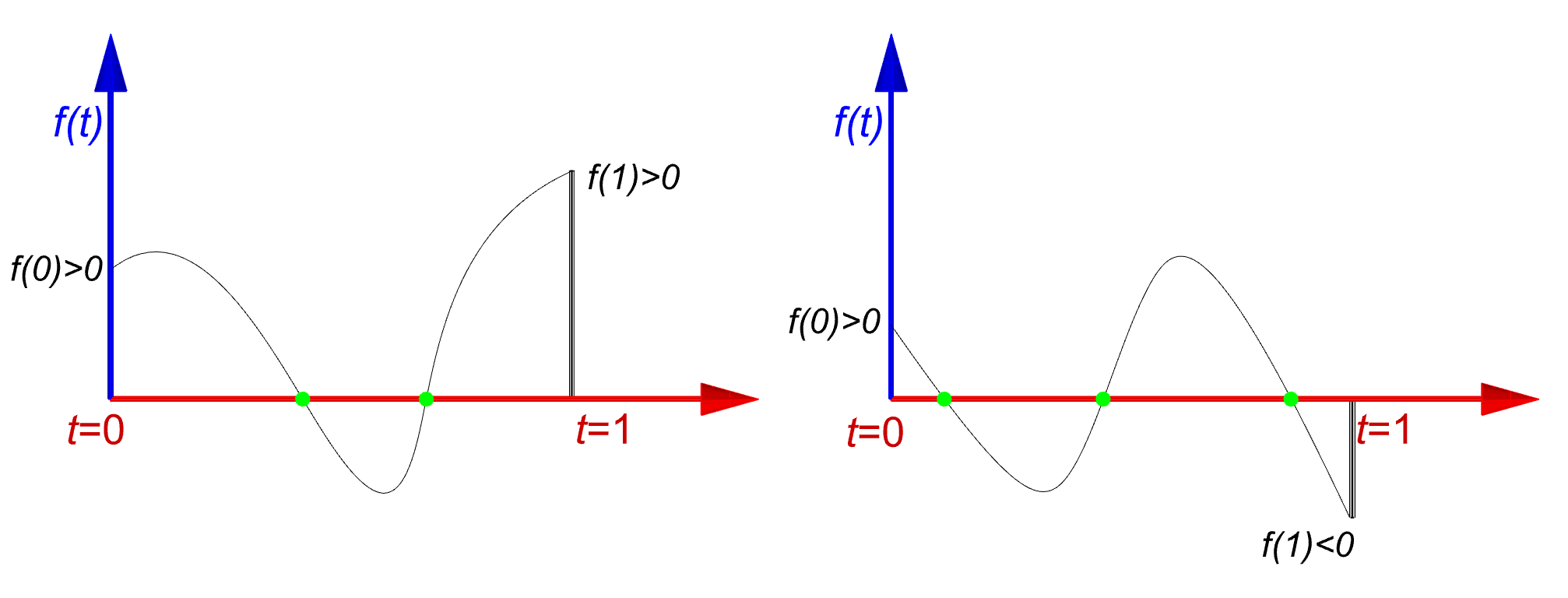
So the algorithm starts with finding an interval like [a,b] as such that f(a)*f(b) <0. We start with the parameter t somewhere with this interval (middle is a good choice t=(a+b)/2) and then verify the stop criteria again for both sub-intervals [a,t] and [t,b] . Note that function f(t) is nothing but the signed distance of the point c(t) from the plane Q , hence we can use the extension method DistanceTo(Plane q,Point p, out projection) which we discussed earlier. 

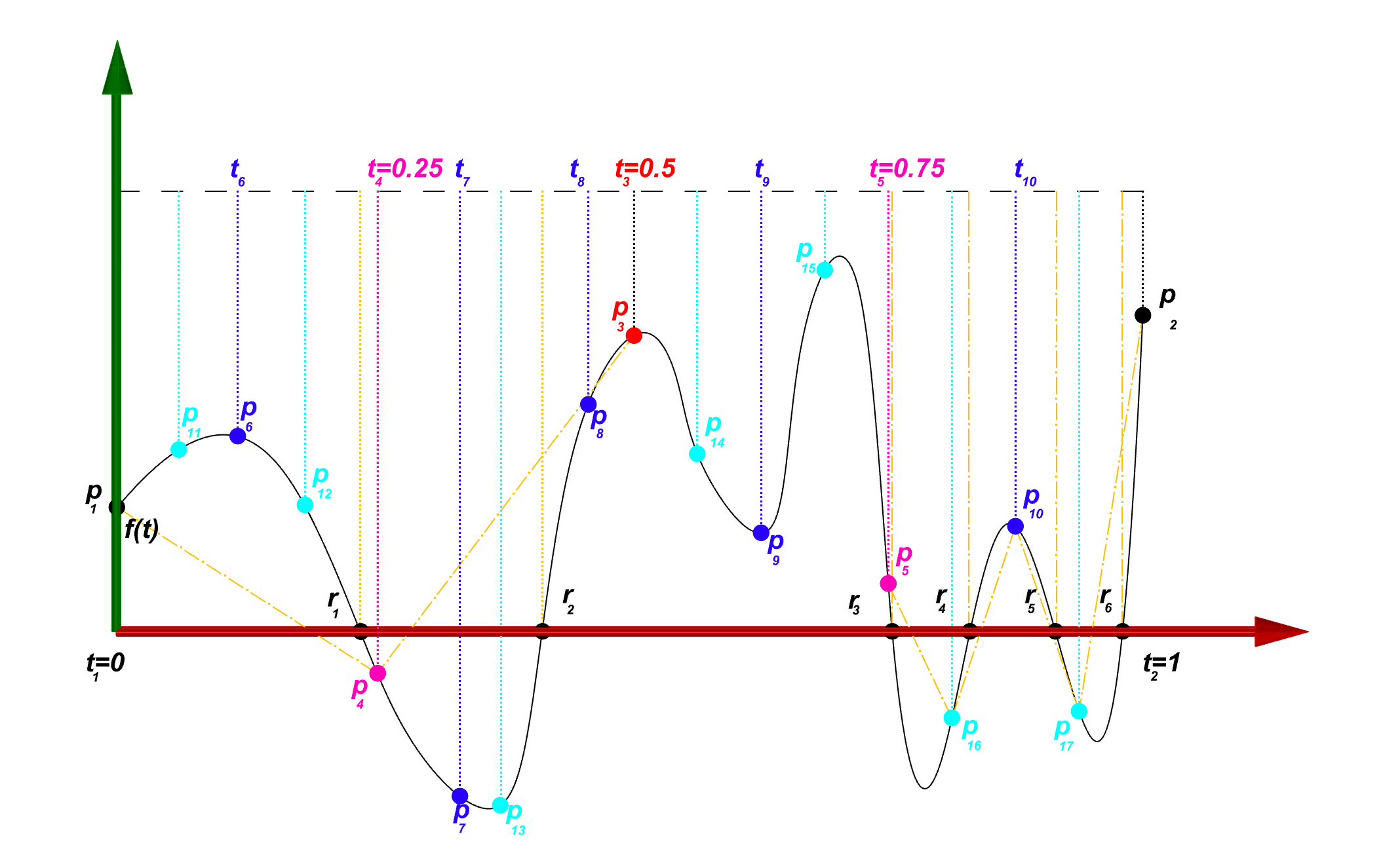
Below graph illustrates an imaginary function f(t) across the domain [t₁,t₂] and we are interested in finding the roots. From the illustration you can see the function intersect the line y=0 in 6 distinct positions. We first check the sign of f(t₁)*f(t₂). since the sign is positive then we cannot insure if there is a root in domain [t₁,t₂] despite the fact that is obvious in the image. Therefore algorithm divides the interval [t₁,t₂] into two sub-domains [t₁,t₃] and [t₁,t₂] where t₃ = (t₁+t₂) /2.0. 

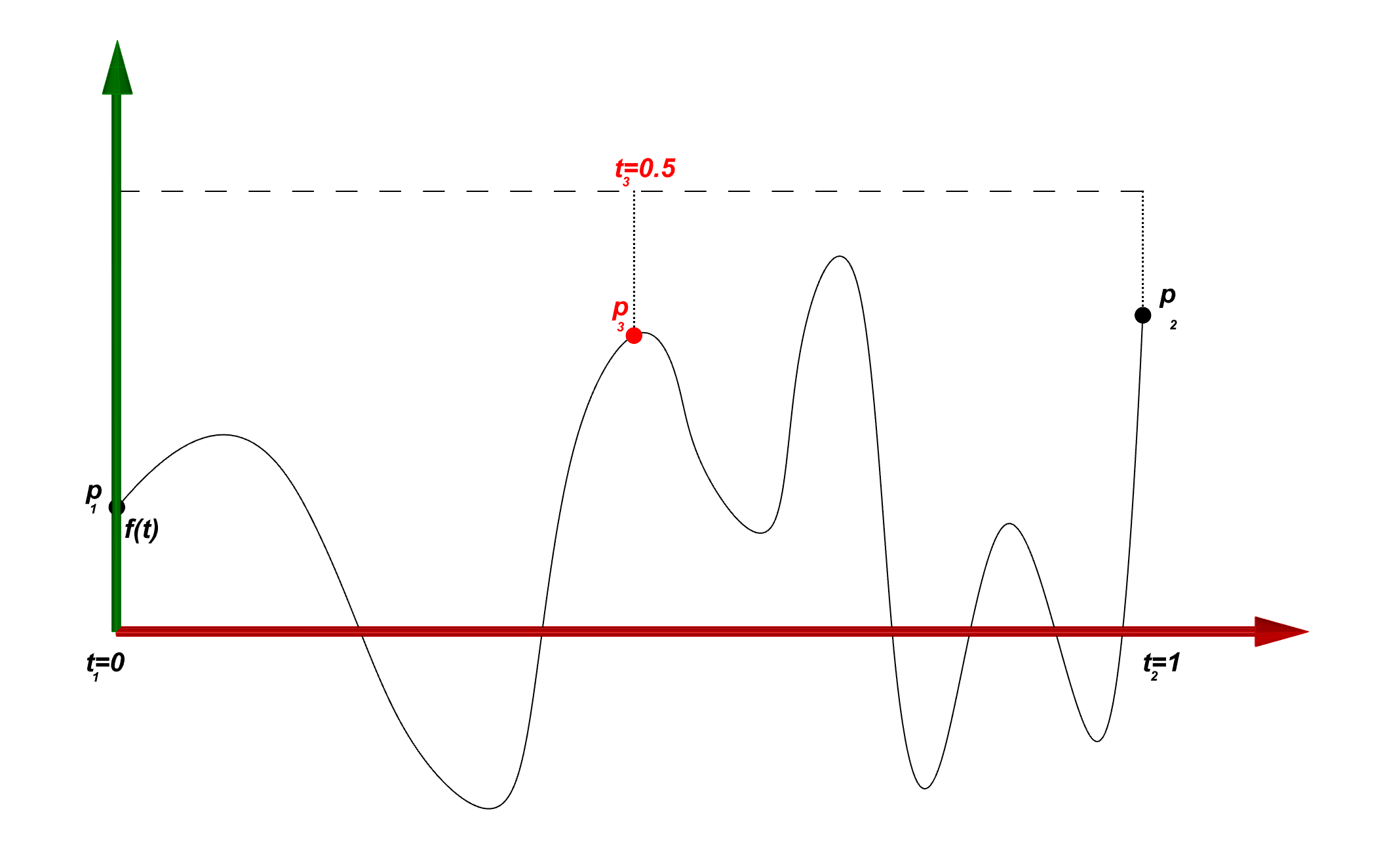
Now algorithm runs again in each sub-domain and check for the sign of function in both ends. Again in the both domains we have f(t₁)*f(t₃)>0 & f(t₃)f(t₂)>0 . Both domains are divided again and send it back as new inputs to our recursive algorithm.

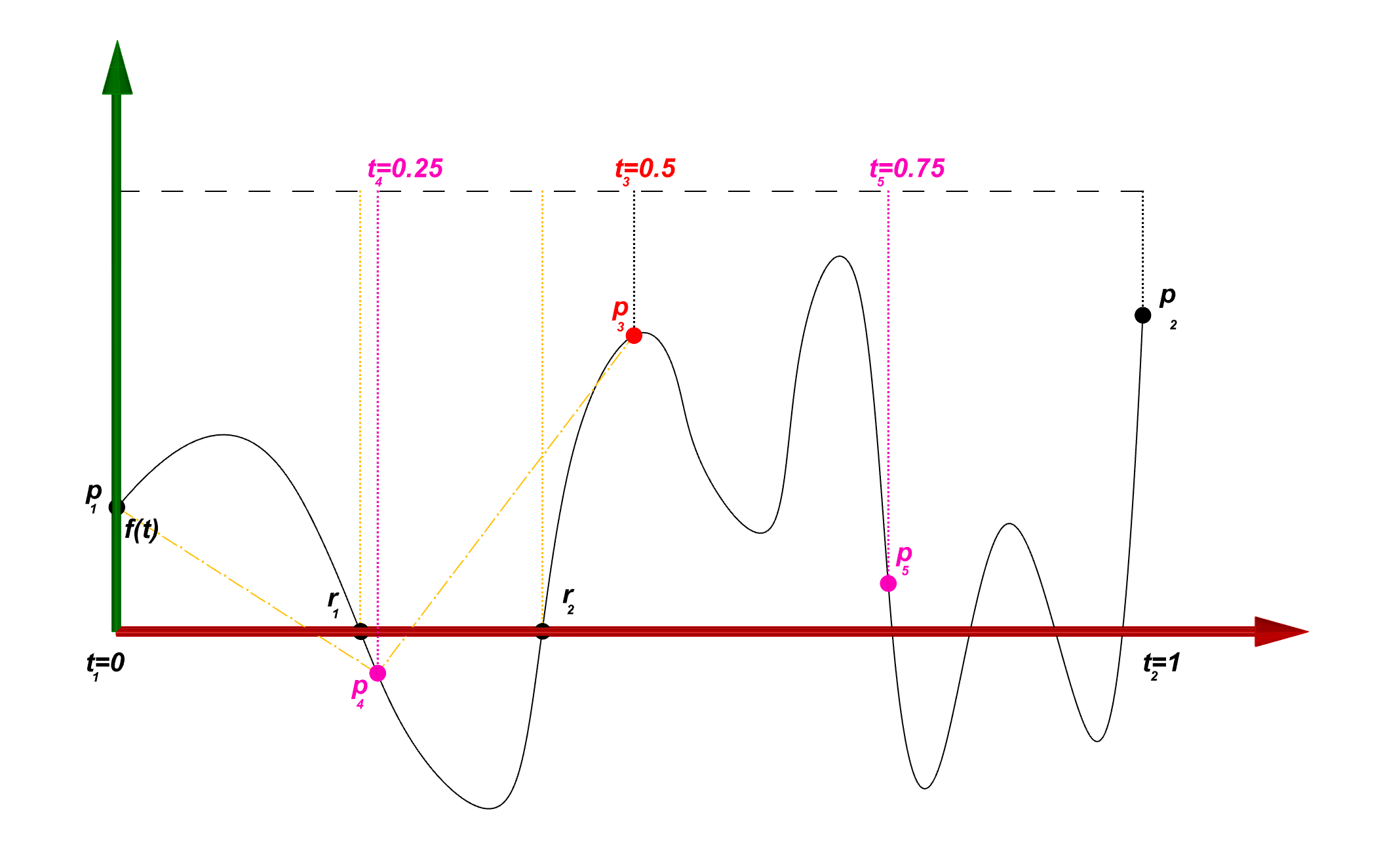
In the new domains [t₁,t₄] and [t₄,t₃] we can see the f(t₁)*f(t₄)<0 and f(t₄)*f(t₃)<0 which means there is at least one root in each sub-domain.  Algorithm shall now switch to root finding routine and find the nearest root to the guess point. To be consistent with the main algorithm we also use the mid point for our root finding algorithm and start the search from the point t₆ = (t₁+t₄)/2 and similarly for the interval [t₄,t₃] from the point p₇ . On the other side the interval [t₃,t₅] and [t₅,t₂] are yet have positive sign for in both ends so they must be divided further.

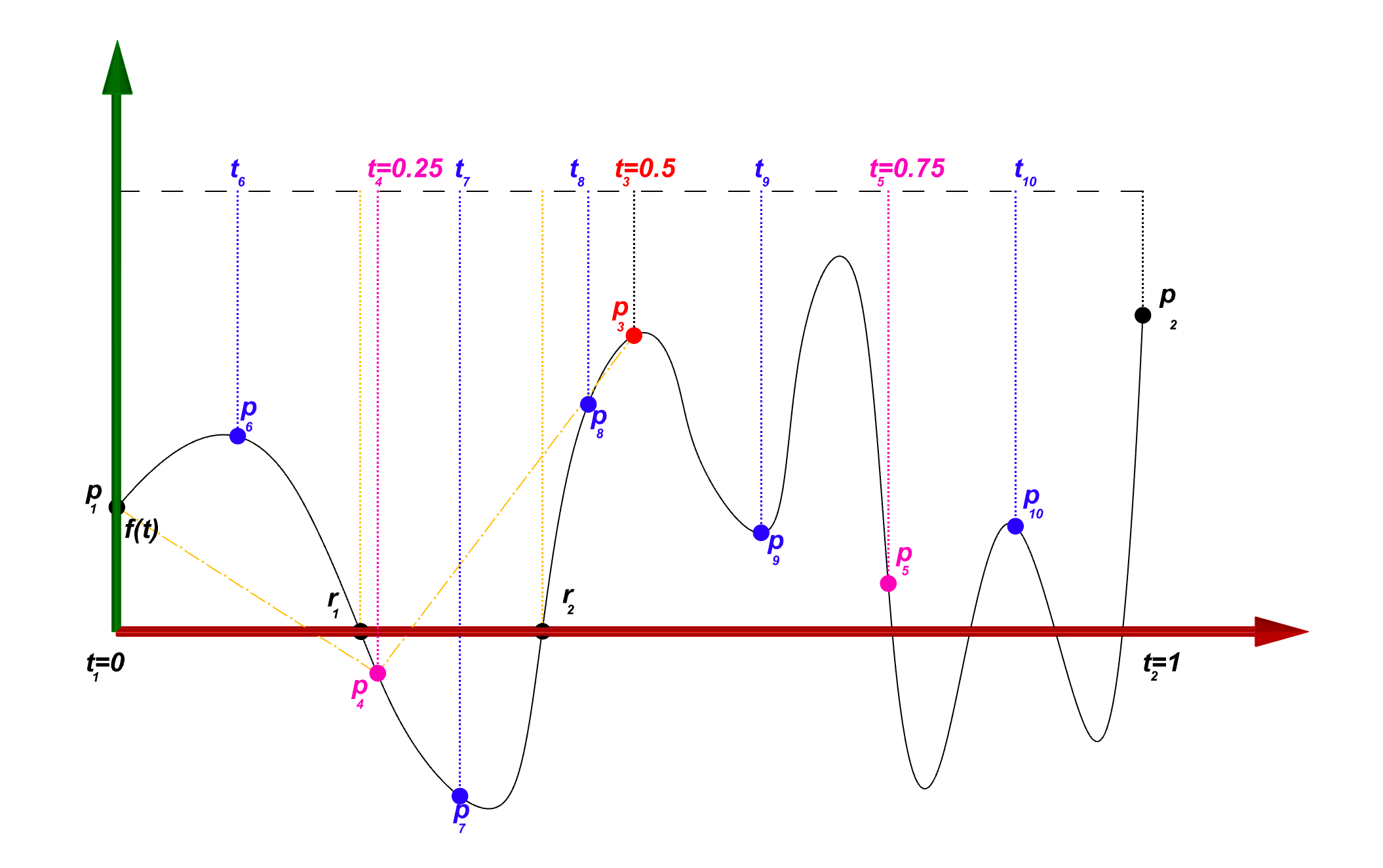
Now that root finding algorithm found the two roots r₁ and r₂ should we continue the sub-division process? well , Yes! as it was shown before there could any odd number of roots in the interval and not only one. In this case we cannot sub-divide the domain from the middle as we may end up finding the same root again. One solution is to divide the domain at the position of the root. In this case the sign of f(t₁)*f(r₁) and f(r₁)*f(t₄) is not useful as it is always returns zero (f(r₁ ) = 0) . In this scenario we need to develop a new criteria to stop the search. looking at the below illustration for we can see a curve starts at point p on one side of the plane and ends on point r which is in the plane Q. For this curve to intersect the line plane Q in more than one location it is necessary to be longer than the line connecting the point p to point r.

The difference in length of the curve C and line l cannot be less than Application.ShortCurveTolerance since this is the length of the shortest curve that is possible in Revit. Here we can update our criteria where at one side of the domain the function is zero.

Still the recursive algorithm can end up in an infinite loop! because the subdivision can go on and on for the portion of curve that is not intersecting the plane as f(a)*f(b) is always positive. We could stop the recursion with the same condition however with both points f(a) and f(b) on one side of y=0 we can do a better job. 

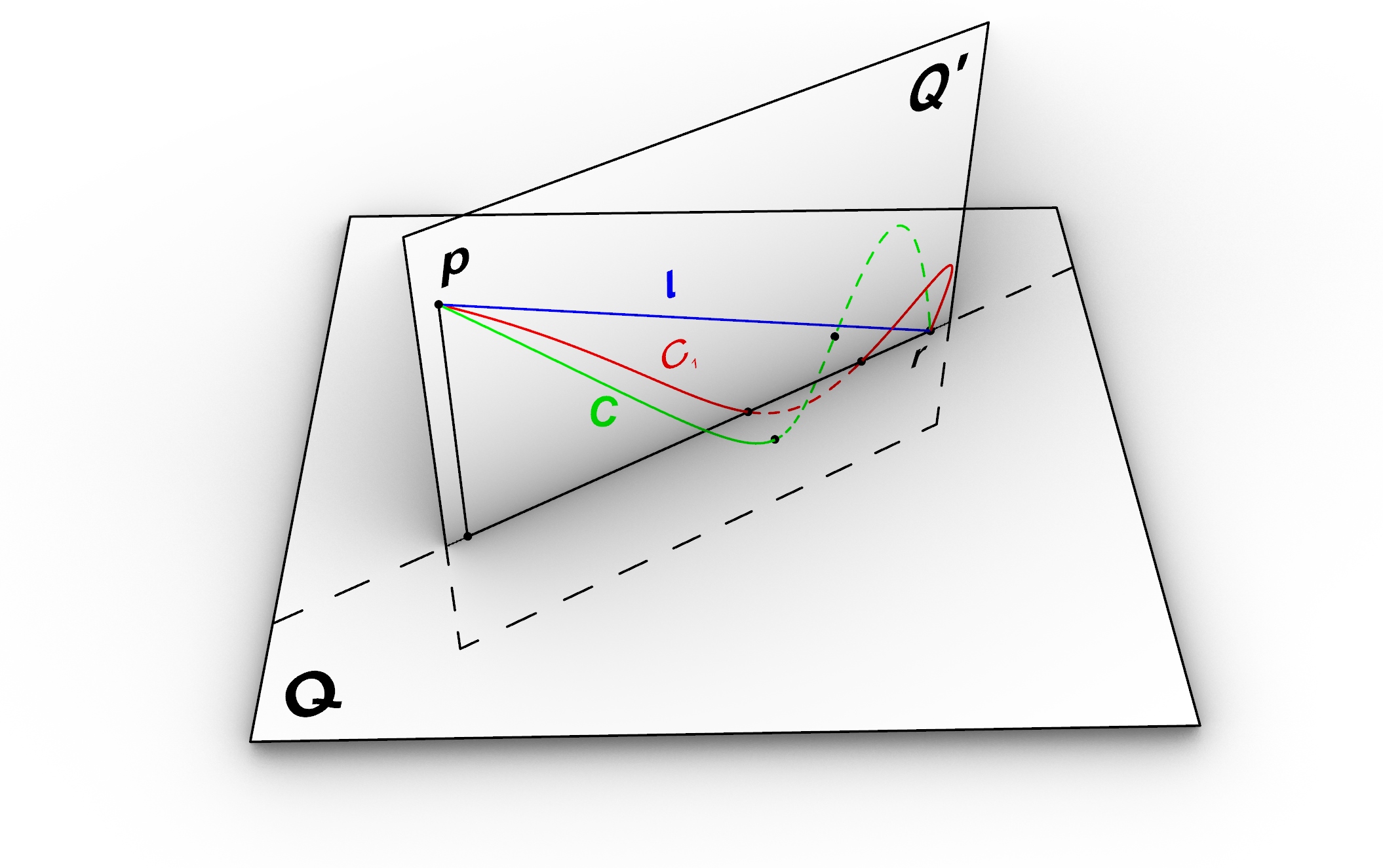
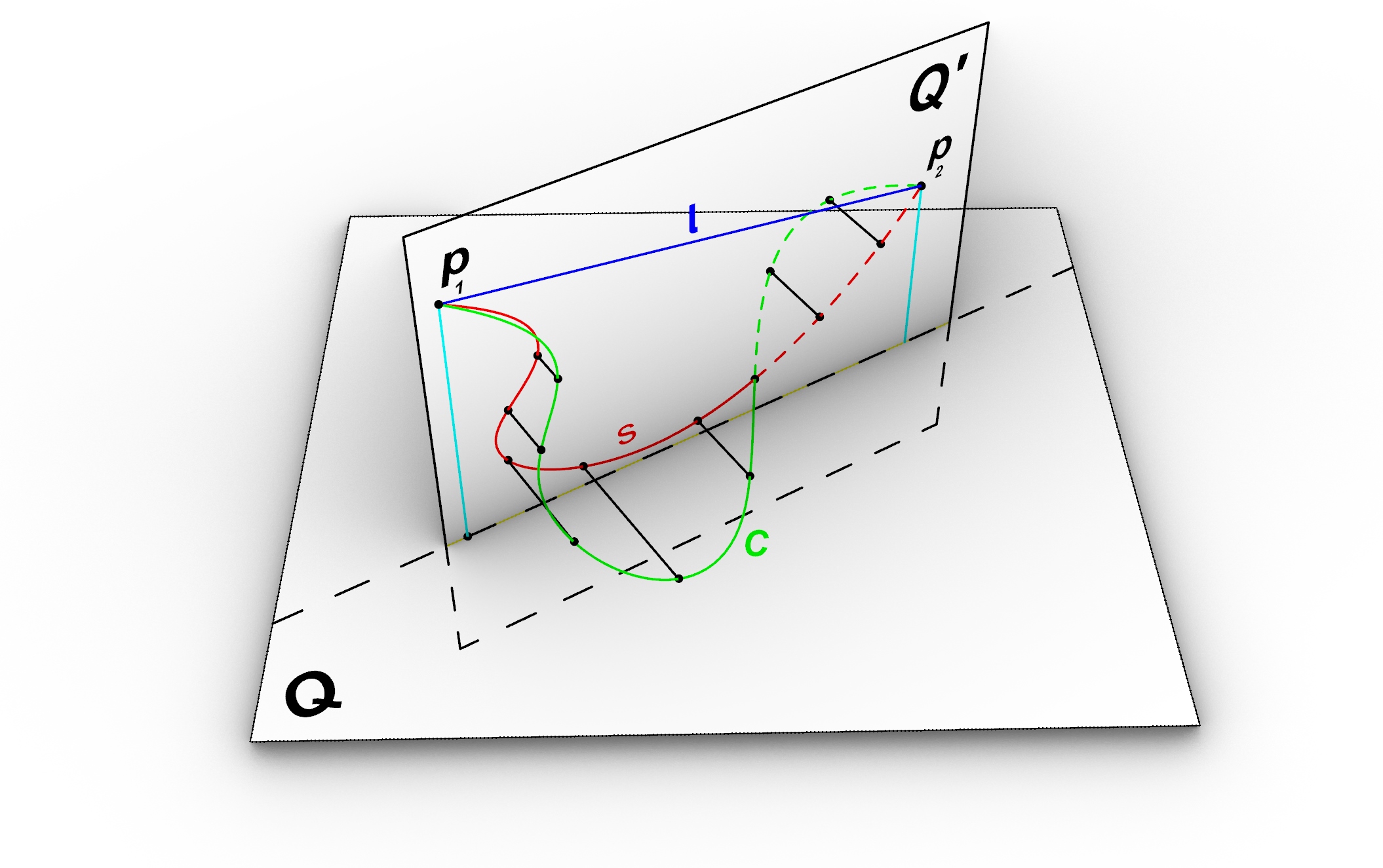
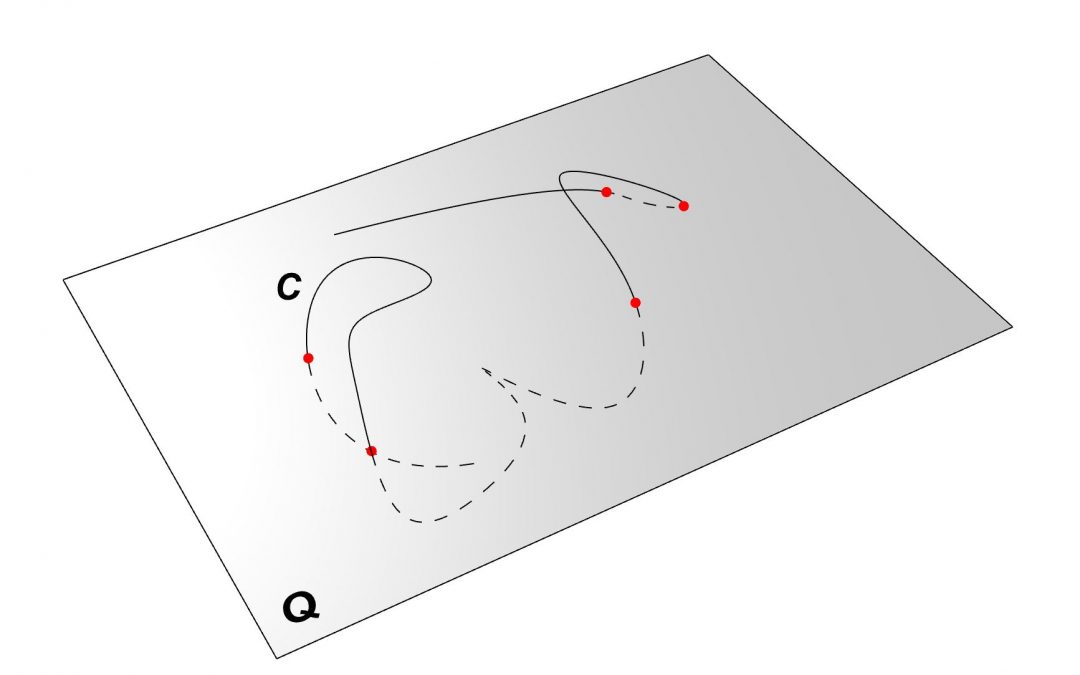
In below illustration the plane Q’ is defined as a plane which contains to end points of the curve C and perpendicular to the plane Q. we would like to project the curve C on plane Q’ and proof that length of the projection curve S is shorter than the length of the original curve C.

Fist we write the length function L(s) and L(c) for both curves:

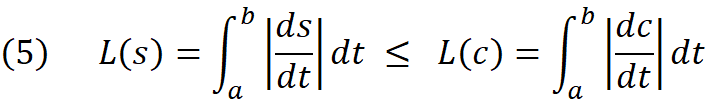
Above is equivalent to below which means all we need to proof is that the inner product of S’ is always smaller than inner product of C’

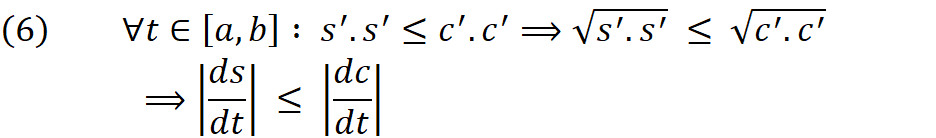
To find the projected curve we move all the points of the curve C along the normal direction of projection plane (Q’) by the signed distance (Equation 3) . Note that the n is the normal of the projection Plane.

Below we compute the derivative of S with respect to curve parameter t and its inner product  

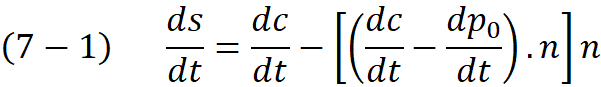
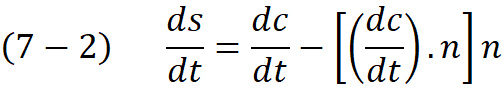
In equation number (9) it is obvious that inner product of S’ is less than inner product of C’ because the (C’.n)² is always positive , hence we proofed that L(C) ≥ L(S)

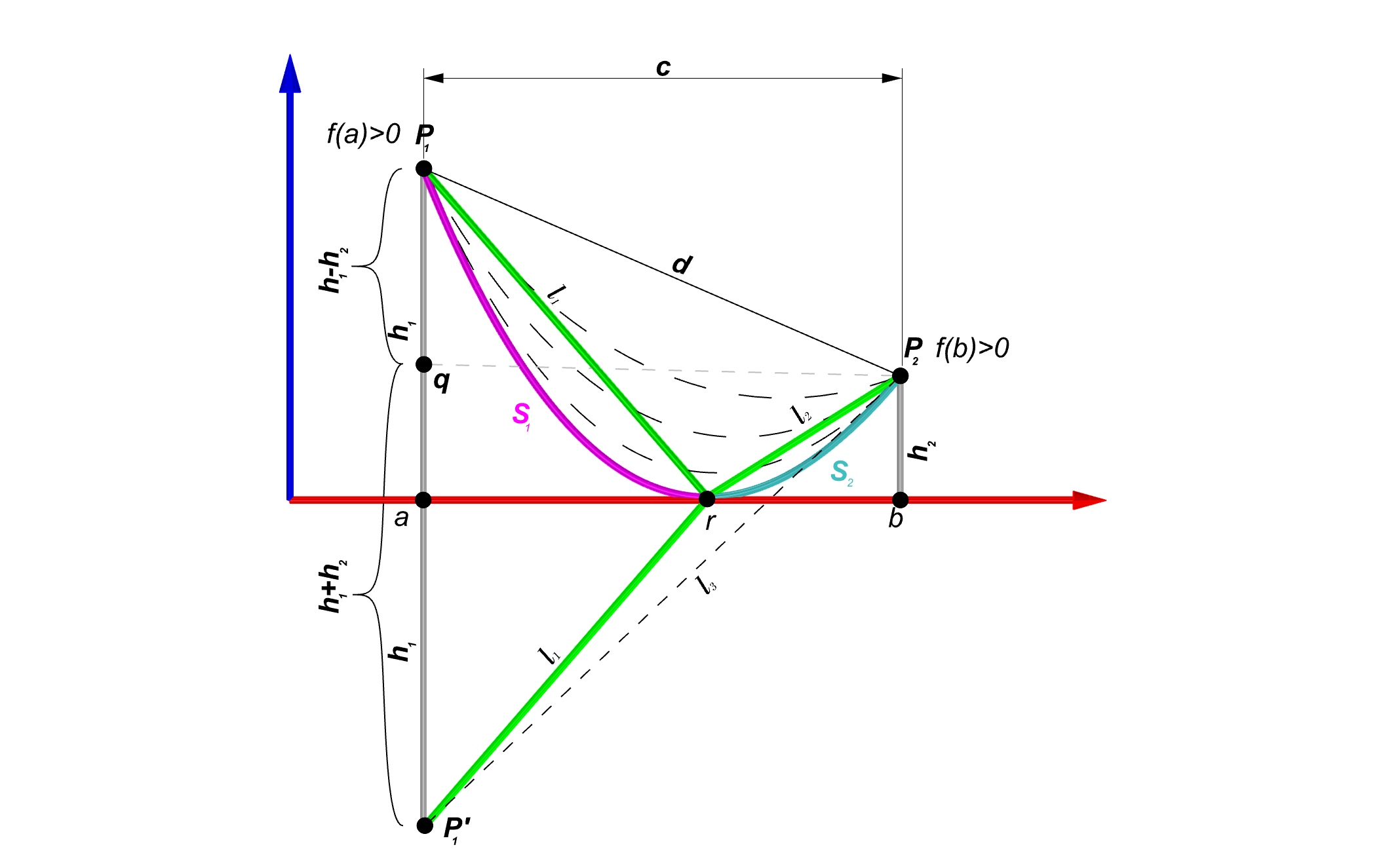
Now instead of the actual Curve C we consider its projection on the plane Q’ and look for a point which curve S contacts the plane. In below illustration the length of the curve S is sum of the the length of Curve S₁ and S₂ hence we can write 

We know that the shortest path between two points on a plane is always the straight line connecting them. therfore we can re-write equation (10) as below:

Let’s find the mirrored image of point P₁ with respect to the line y=0 and call it point p’₁ and also point q find the projection of point p₂ on the line connecting p₁ to p’₁.  We draw a line connecting p₂ and p’₁ with length of l₃. From the triangle inequality theorem , It is also known that in a triangle the sum of two edges is always greater or equal to the third edge.  therefore : 

Two triangles  q,p’₁,p₂ and q,p₂,p₁ are right angle, hence from Pythagorean theorem we can write :

By substituting the c₂ from the right equation we then achieve :

And finally we find a minimum length for the curve C , we can use this term as stop criteria 

Notice that if one of the terms h₁ or h₂ are zero our condition reduces to simple comparison between the curve length and line length which we used before, therefore it is not a bad idea to replace the previous condition with the new one. In below you can see that condition for both scenarios are combined into one. 

Now the algorithm stops when the sub-curve is not long enough to make an intersection with the plane. For example as shown in below illustration the curve segment between p₉ and p₁₅ will be subdivide till the length of the seghemt reach the treshold given by equation (11)  

Below you can find the entire implementation of the method. This method works well for less number of intersections. When it comes to massive number of intersections it may suffer in performance, however you can increase the speed by  making the search slightly less accurate and using bigger value for the epsilon (maximum distance from the point to the plane). In the next post we discuss a simpler but more robust method which uses some Revit API native methods to compute the intersection.