A simple problem :
Fit a flat set of points on XY plane into a given rectangle. Or in other words place the given rectangle around the set of points which contains all the points. In the same time determine if the problem has a solution or not?
In this video I used Rhino+Grasshopper….
Note that this problem is different than finding the minimum bounding rectangle of the poly-line which can be solved using Rotating calipers.
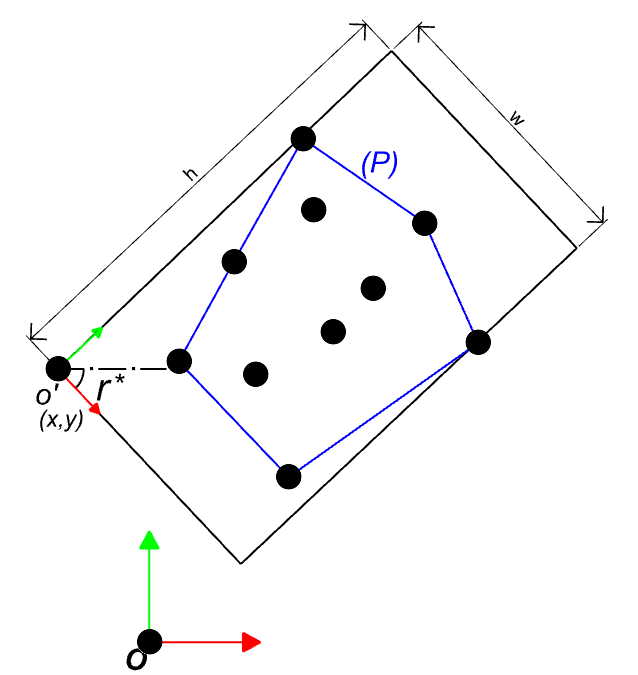
In this problem we don’t need to find the rectangle but, find the transformation which places all the points inside the rectangle. Such that transformation has two components, Rotation and Translation. In a 2D problem we can reduce the unknown to three variable r,x and y which represent the rotation amount (r) , and the x and y coordinates of the translation vector. Before we start thinking of a solution , we can reduce the problem further using convex hull of the points instead of the point set itself , simply because any points inside the convex hull will be automatically inside our rectangle.
We define transformation A which transform all points of the convex hull P into a set Q:
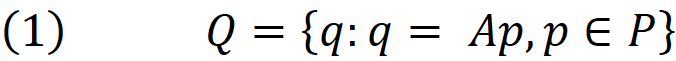
In order for all points in Q to be inside the rectangle (W,H) where W is the width along X axis and H is the height along Y axis, the following must be held for all points:
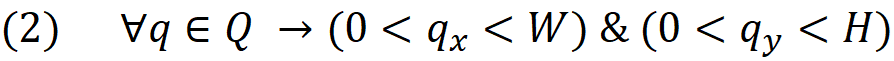
In above qₓ and qᵧ are the X and Y coordinates of the point q. This is shown in the images below.
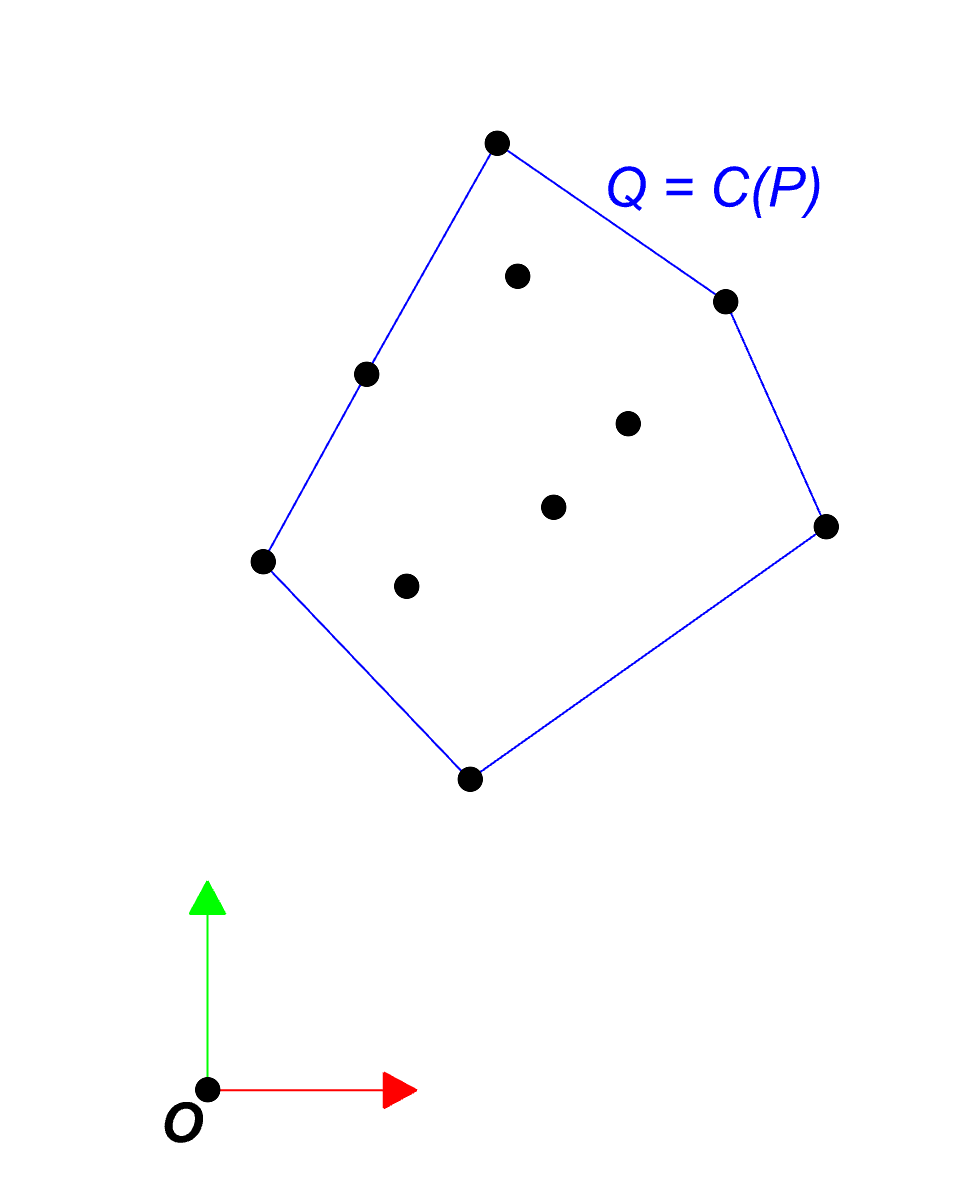
The left image shows the convex hull P before transformation and in the right image you find the set Q after transformation in which all points are within the rectangle (W,H):
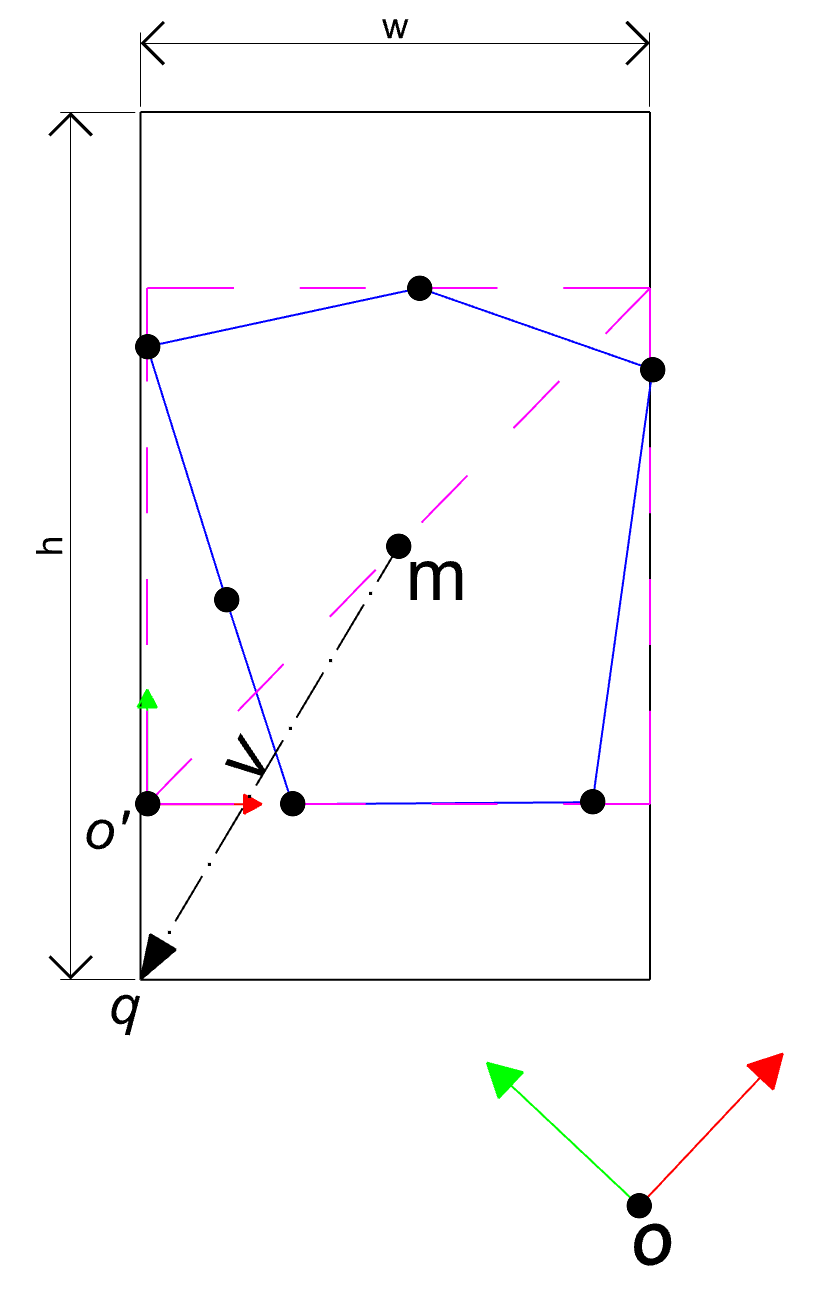
Now we write the transformation A as product of its two component Tₓ,ᵧ for translation and Rᵣ for rotation . Note that T is a function of x and y and R is a function of r, therefore we use the subscripts x,y and r to indicate that matrices T and R are depending on these variables.
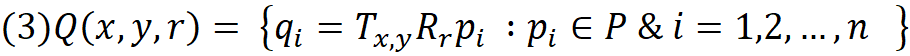
We find the minimum rectangle along X and Y axis which contains all the points in Q. This can be achieved by creating two sets of real numbers from x and y components of the points in set Q.
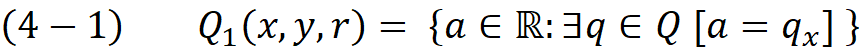
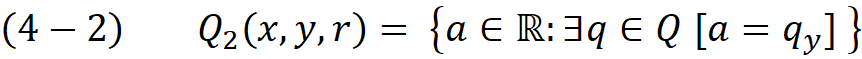
The width of the min-rectangle is the difference between min and max in the set Q₁ and in the same way the height of the min-rectangle could be found in set Q₂.
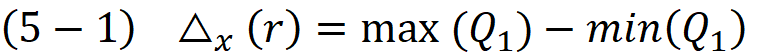
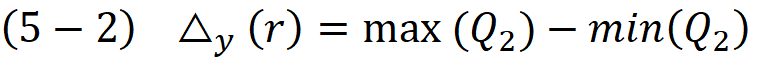
Notice that the function Δ(r) is independent from the x and y variables.This is quiet obvious because the translation has no effect on the distance between the min and max point, in other words the displacement T moved the min point with the same amount and in the same direction as the max point , therefore it will cancel out in equation (5-1) and (5-2).
Below image demonstrate the function Δₓ(r) and Δᵧ(r) :
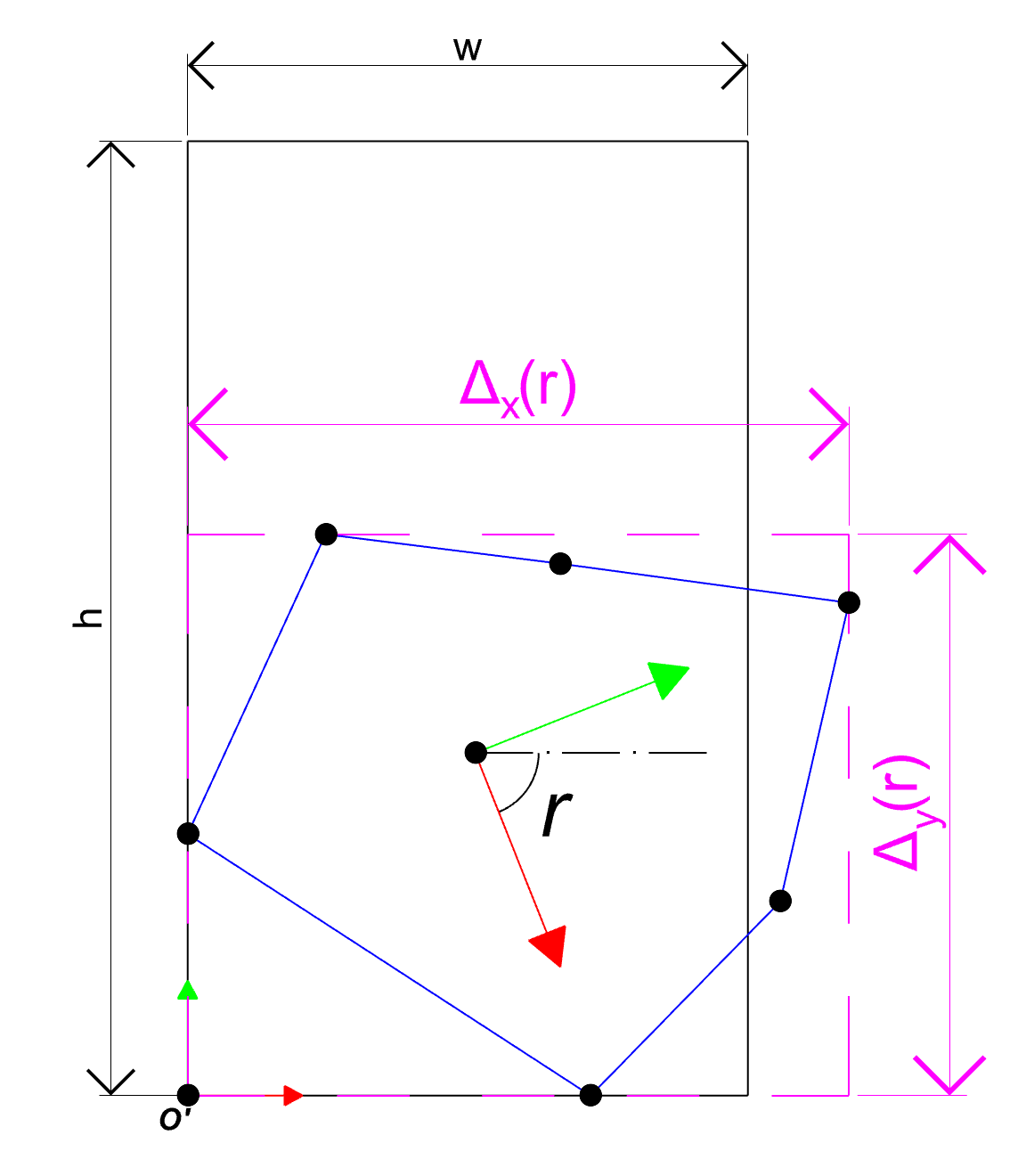
The aim is find such r that the rectangle ( Δₓ(r) , Δᵧ(r) ) as such that it fits inside the given rectangle (W,H) , hence we can write :
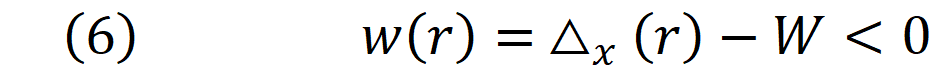
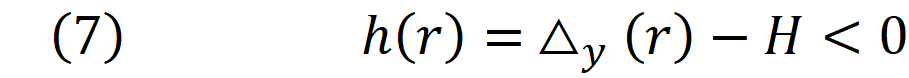
₀This is a non-linear system of inequalities which can be solved by minimizing both w(r) and h(r) till both inequalities are satisfied. Looking at equations 5-1 and 5-2 it is also clear that the problem is non-differentiable. The points that function are not differentiable is actually the points where one of the edges of convex hull P is aligned with either X or Y axis. To overcome this problem we must divide the domain of the function into the intervals which the bounding rectangle moves smoothly. This can be done by subdividing the domain at angles between one edge to the other. Note that the domain for r does not have to be [0,2π ]. this is because rotating the poly-line P by 90 degree will swap the values of w(r) and h(r) , therefore we can limit our search safely to the domain [0,π] .
In the future posts I propose an algorithm for solving the inequalities (6) and (7) and dividing the problem to a series of sub-domains where both functions are differentiable. Till then stay tuned….

Recent Comments