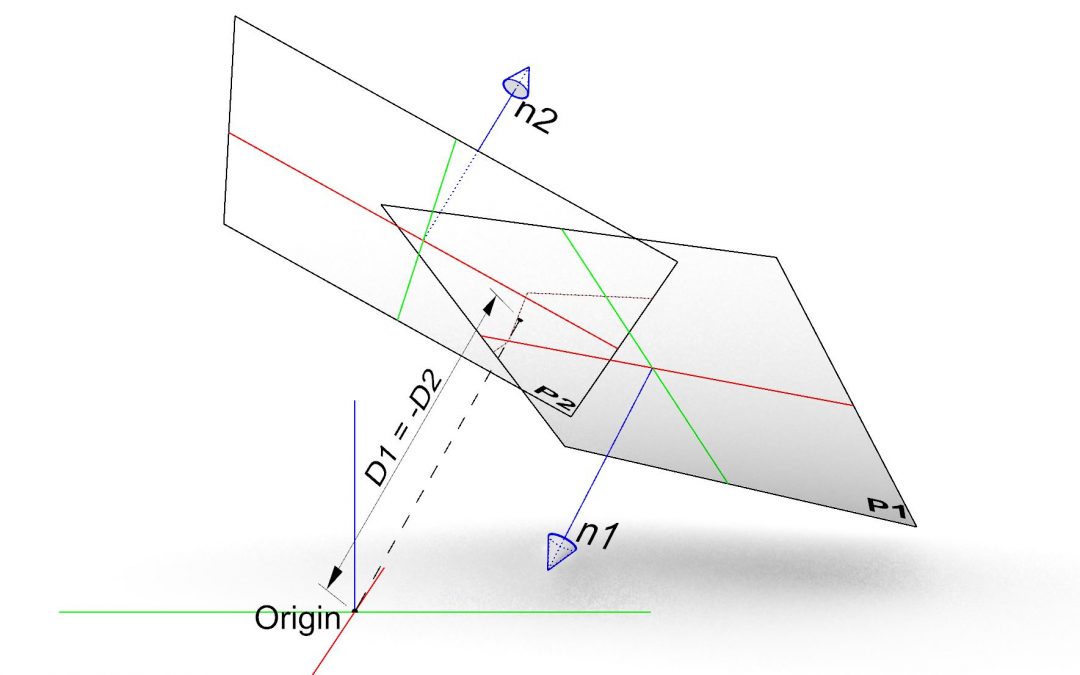
Further to my previous post about signed distance to plane , Here I would like to share another insight to plane geometry in Revit API. Two planes are geometrically the same (they are coincident) if all points are one plane lies on other plane too. At first you may think you can simply test if they are equal by calling the Equal() method. Although the equal planes are certainly coincident , but there are coincident planes that are not equal by formulation. Let’s look at the mathematical definition of the plane:
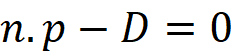
Where n is a unit normal vector to the plane, p is a position vector of a point of the plane and D the signed distance of the plane from the origin. This definition is known as the Hesse normal form relies on the parameter D. Now let us say two planes P₁ and P₂ are coincide, this means equations for both planes must be satisfied regardless of the position vector p . In the other words if point p satisfies the first equation then it should also satisfies the second one :
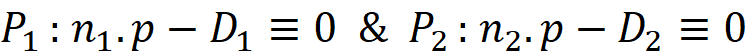
There are two sets of trivial solutions in which both equatios are statisfied:
In case (1) the normal vectors of two planes are identical and the planes are having the same distance from the origin. In case (2) the normal of P₂ is the reverse of the normal of P₁ and the signed distance of P₁ is the negative of the signed distance of the P₂. Now let us implement above conditions in Revit API by looking at Plane class. There are two essential properties of the plane that we need to compare. First, the normal vector which must be in unique length. Considering both cases (1) and (2) we compare the normal vectors in both direct and reverse direction:
if (p1.Normal.IsAlmostEqualTo(p2.Normal) || p1.Normal.IsAlmostEqualTo(-p2.Normal))
{
//if above condition is satisfied then planes are parallel
}
Note that vectors are compared using IsAlmostEqualtTo not the Equality method. If above conditions are statisfied then it means the planes are parallel, The next step is to compare the parameter D or the signed distance from the origin. This is not implemented in Revit API but it can be easily retrieved from the dot product of the normal plane and the a point on the plane. looking at the plane equation again we can write :
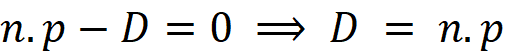
For the point p on the plane we can choose the Origin and to cover the both cases (1) and (2) we only compare the absolute value of parameter D. Similar to vector comparison, we need to take into account that numbers could be very close but still not equal, therefore it is wised to consider a tolerance value. Here we use an arbitrary tolerance which must be sufficiently small :
// if both planes are parallel then check if they have the same distance to the origin.
double d1 = Math.Abs(p1.Origin.DotProduct(p1.Normal));
double d2 = Math.Abs(p2.Origin.DotProduct(p2.Normal));
return (Math.Abs(d1 - d2) < tolerance);
Choosing the tolerance value is quite relative. In our implementation the tolerance is actually the maximum distance between two parallel planes which must be considered coincident. To be consistent with the method IsAlmostEqualTo() , a good choice could be (10e-9) . Here is the full implemenation :
/// <summary>
/// Returns true if the plane p2 lies on this plane (p1).
/// </summary>
/// <param name="p1"></param>
/// <param name="p2"></param>
/// <param name="tolerance">if distance between two parallel planes is less than
/// this threshold then they are considered as Coincide planes</param>
/// <returns></returns>
public static bool IsCoincident(this Plane p1 , Plane p2, double tolerance)
{
// check if the normal of this plane is equal (or reverse ) to the normal of the other Plane
if (p1.Normal.IsAlmostEqualTo(p2.Normal) || p1.Normal.IsAlmostEqualTo(-p2.Normal))
{
// if both planes are parallel then check if they have the same distance to the origin.
double d1 = Math.Abs(p1.Origin.DotProduct(p1.Normal));
double d2 = Math.Abs(p2.Origin.DotProduct(p2.Normal));
// the difference between d1 and d2 must be within given tolerance
return (Math.Abs(d1 - d2) < tolerance);
}
else
{
return false; // if planes are not parallel then they cannot be coincide
}
}

Recent Comments